Syllabus: [pdf]
Exams
Exam 1: [pdf] [tex]
Exam 2: [pdf] [tex]
Exam 3: [pdf] [tex]
Homework
Homework 1 (due 26 August) (solution: [pdf]): click here
Homework 2 (due 4 September) (solution: [pdf]): click here
Homework 3 (due 9 September) (solution: [pdf]): click here
Homework 4 (due 16 September) (solution: [pdf]): click here
Homework 5 (due 2 October) (solution: [pdf]): click here
Homework 6 (due 9 October) (solution: [pdf]): click here
Homework 7 (due 14 October) (solution: [pdf]): click here
Homework 8 (due 23 October) (solution: [pdf]): click here
Homework 9 (due 30 October) (solution: [pdf]: click here
Homework 10 (due 11 November) (solution: [pdf]): click here
Homework 11 (due 18 November) (solution: [pdf]): click here
Homework 12 (due day of final exam) (solution: [pdf]): click here
Quizzes
Quiz 1 (due 28 August) (solution: [pdf]): Write in polar form and multiply $z_1=-2$ and $z_2=3$.
Quiz 2 (due 27 September) (solution: [pdf]): Use the logarithm definition of the principal $\mathrm{Arccos}$ function to compute $\mathrm{Arccos}\left( \dfrac{1}{2} \right)$.
Quiz 3 (due 9 October) (solution: [pdf]): Calculate $\displaystyle\int_C \overline{z} \mathrm{d}z$ where $C$ is the contour $\left\{ \begin{array}{ll}
z(t)=2e^{it} \\
-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}.
\end{array} \right.$
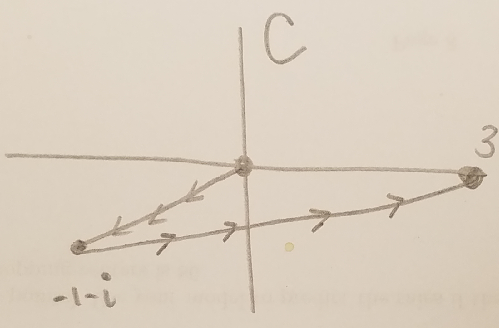
Quiz 4 (due 14 October) (solution: [pdf]): Recall that to parametrize a line segment from $a+bi$ to $c+di$ use $\left\{ \begin{array}{ll} z(t)=t(c+di)+(1-t)(a+bi) \\
0 \leq t \leq 1 \end{array} \right.$. Use this to parametrize the curve $C$ appearing below and compute $\displaystyle\int_C \mathrm{Re}(z) \mathrm{d}z$.
Class notes
Notes for week 1
Notes for week 2-3
Notes from week 3-4
Notes from week 4
Notes from week 6
Notes from week 7
Notes from week 8
Notes from week 9
Notes from week 10-11
Other stuff
Mobius transformations revealed by Douglas Arnold and Jonathan Rogness
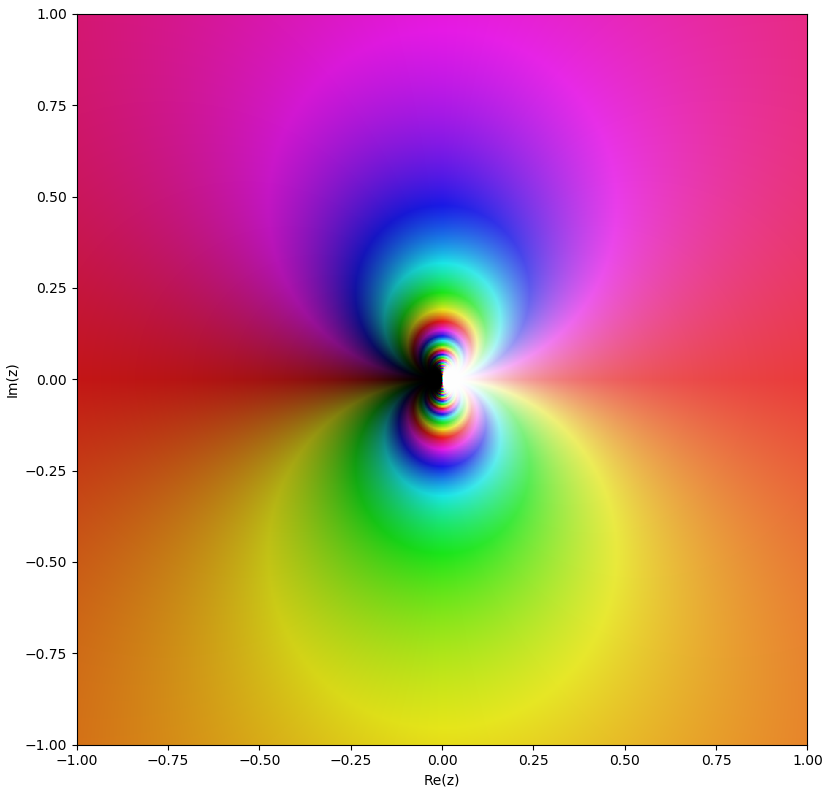
Domain coloring of $e^{\frac{1}{z}}$: (almost) all colors appear in every circle around the "essential singularity" at $z=0$, demonstrating the Great Picard Theorem