Syllabus
Online Homework
For Exam 1 (ultimately due 5 February)
HW1: Algebraic Expressions (recommended due date 17 January)
HW2: Equations and inequalities and exponents and radicals (recommended due date 24 Jan)
For Exam 2 (ultimately due 4 March)
HW3: Functions (recommended due date 12 Feb)
HW4: Exponentials and logarithms (recommended due date 14 Feb)
HW5: Limits (recommended due date 19 Feb)
HW6: Intro to differentiation (recommended due date 21 Feb)
HW7: Deriatives of common functions (recommended due date 26 Feb)
For Exam 3 (ultimately due 8 April)
HW8: Product and quotient rules (recommended due 6 March)
HW9: Chain rule and implicit differentiation (recommended due 13 March)
HW10: Related rates (recommended due date 18 March)
HW11: Optimization (recmomended due date 21 March)
For final exam (ultimately due 27 April)
HW12: Antidifferentaition
HW13: Integration
HW14: Fundamental theorem of calculus
Quizzes
For Exam 1
Quiz 1 (due 18 Jan in Blackboard) [soln]: Add $\dfrac{2}{x+7}+\dfrac{3x}{x+2}$.
Quiz 2 (due 25 Jan in Blackboard) [soln]: Solve the rational equation $\dfrac{5}{p-2}-\dfrac{7}{p+2}=\dfrac{12}{p^2-4}$.
For Exam 2
Quiz 3 (due 6 Feb in Blackbaord) [soln]: Given $h(\phi)=(\phi-1)^2+\phi$, compute $h(2)$, $h(5)$, and $h(x+1)$.
Quiz 4 (due 13 Feb in Blackboard) [soln]: Find (if it exists) these four things: $\displaystyle\lim_{x\rightarrow 3^{-}} f(x)$, $\displaystyle\lim_{x \rightarrow 3^+} f(x)$, $\displaystyle\lim_{x\rightarrow 3} f(x)$, and $f(3)$ in the following graph:
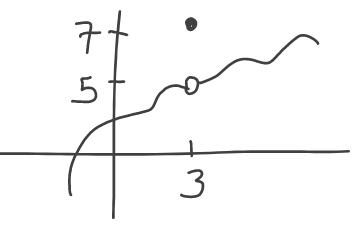
Quiz 5 (due 17 Feb in Blackboard) [soln]: Tell me where the curve has a positive derivative:

Quiz 6 (due 22 Feb in Blackboard) [soln]: Compute the derivative of $h(x)=7x^2-5x+4$.
For Exam 3
Quiz 7 (due 7 Mar in Blackboard) [soln]: Compute $\dfrac{\mathrm{d}}{\mathrm{d}x} \left[ \dfrac{xe^x}{\ln(x)} \right]$.
Quiz 8 (due 14 Mar in Blackboard) [soln]: Let $f(x)=2x^2-5x+2$. Find and classify all local extrema of $f$.
Quiz 9 (due 12 Apr in Blackboard) []: Given that $\displaystyle\int_2^5 f(x) \mathrm{d}x = 3$ and $\displaystyle\int_7^5 f(x) \mathrm{d}x = -2$, compute $\displaystyle\int_2^7 10f(x) \mathrm{d}x$.
Exams
Exam 1
Exam 2
Exam 3





