Back to the class
Section 8.3 #4: $$\displaystyle\int \sin^3(3x) \mathrm{d}x$$
Solution: Recall the Pythagorean identity
$$\cos^2(\theta) + \sin^2(\theta)=1.$$
We applying this rearranged to $\sin^2(\theta)=1-\cos^2(\theta)$ with $\theta=3x$ yields
$$\sin^3(3x) = \sin(3x) \sin^2(3x) = \sin(3x) (1-\cos^2(3x)).$$
Therefore we may compute
$$\begin{array}{ll}
\displaystyle\int \sin^3(3x) \mathrm{d}x &= \displaystyle\int \sin(3x) \left( 1-\cos^2(3x) \right) \mathrm{d}x \\
&= \displaystyle\int \sin(3x) \mathrm{d}x - \displaystyle\int \sin(3x) \cos^2(3x) \mathrm{d}x \\
&\stackrel{u_1=3x,u_2=\cos(3x)}{=} -\dfrac{1}{3} \displaystyle\int \sin(u_1) \mathrm{d}u_1 + \dfrac{1}{3} \displaystyle\int u_2^2 \mathrm{d}u_2 \\
&= \dfrac{1}{3} \cos(u_1) - \dfrac{1}{9} u_2^3 + C \\
&= \dfrac{1}{3} \cos(3x) - \dfrac{1}{9} \cos^3(3x) + C.
\end{array}$$
Section 8.3 #9: $$\displaystyle\int \cos^2(3x) \mathrm{d}x$$
Solution: Recall the "reduction" identity
$$\cos^2(\theta) = \dfrac{1+\cos(2\theta)}{2}.$$
Apply that identity with $\theta=3x$ to see
$$\cos^2(3x) = \dfrac{1+\cos(6x)}{2}.$$
Therefore compute
$$\begin{array}{ll}
\displaystyle\int \cos^2(3x) \mathrm{d}x &= \displaystyle\int \dfrac{1+\cos(6x)}{2} \mathrm{d}x \\
&= \dfrac{1}{2} \displaystyle\int 1 \mathrm{d}x + \dfrac{1}{2} \displaystyle\int \cos(6x) \mathrm{d}x \\
&=\dfrac{x}{2} + \dfrac{1}{12} \sin(6x) + C.
\end{array}$$
Section 8.4 #22: $$\displaystyle\int \dfrac{x^2}{\sqrt{36-x^2}} \mathrm{d}x$$
Solution: Recall that the Pythagorean identity may be rearranged to say
$$\sqrt{1-\sin^2(\theta)} = \cos(\theta).$$
Also recall the "reduction" identity
$$\sin^2(\theta) = \dfrac{1-\cos(2\theta)}{2}.$$
Let $x=6\sin(\theta)$ so that $\mathrm{d}x = 6\cos(\theta) \mathrm{d}\theta$. Substituting this variable into the integral yields
$$\begin{array}{ll}
\displaystyle\int \dfrac{x^2}{36-x^2} \mathrm{d}x &= \displaystyle\int \dfrac{36\sin^2(\theta)}{\sqrt{36-36\sin^2(\theta)}} 6 \cos(\theta) \mathrm{d}\theta \\
&= \dfrac{36 \cdot 6}{6} \displaystyle\int \dfrac{ \sin^2(\theta) \cos(\theta)}{\sqrt{1-\sin^2(\theta)}} \mathrm{d}\theta \\
&= 36 \displaystyle\int \dfrac{\sin^2(\theta)\cos(\theta)}{\cos(\theta)} \mathrm{d}\theta \\
&= 36 \displaystyle\int \sin^2(\theta) \mathrm{d}\theta \\
&= \dfrac{36}{2} \displaystyle\int 1 \mathrm{d}\theta - \dfrac{36}{2} \displaystyle\int \cos(2\theta) \mathrm{d}\theta \\
&= 18 \theta - 9 \sin(2\theta) + C.
\end{array}$$
Solving our assignment $x=6\sin(\theta)$ for $\theta$ yields $\theta = \arcsin \left( \dfrac{x}{6} \right)$. Recall the double angle identity
$$\cos(2\psi)=2\sin(\psi)\cos(\psi).$$
Applying this shows us that
$$-9\sin(2\theta) = -18\sin(\theta)\cos(\theta) = -18 \left( \dfrac{x}{6} \right) \cos(\theta) = -3 \cos(\theta).$$
io determine $\cos(\theta)$ we must draw a triangle:
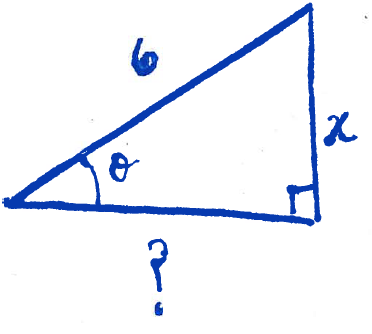
To find the side labelled "$?$", we use the Pythagorean theorem:
$$?^2 + x^2 = 6^2.$$
Solving for $?$ yields
$$? = \sqrt{36-x^2}.$$
Therefore $\cos(\theta) = \dfrac{\sqrt{36-x^2}}{6}$. So, finally, we compute
$$\displaystyle\int \dfrac{x^2}{\sqrt{36-x^2}} \mathrm{d}x = 18 \arcsin \left( \dfrac{x}{6} \right) - 3x \cos(\theta) = 18\arcsin \left( \dfrac{x}{6} \right) - \dfrac{x}{2} \sqrt{36-x^2} +C.$$
Section 8.5 #6: $$\displaystyle\int \dfrac{2}{9x^2-1} \mathrm{d}x$$
Solution: The denominator is a difference of squares (i.e. $a^2-b^2=(a-b)(a+b)$) and so it factors:
$$9x^2-1 = (3x)^2-1 = (3x-1)(3x+1).$$
Therefore, we must apply partial fractions to
$$\dfrac{2}{9x^2-1} = \dfrac{A}{3x-1} + \dfrac{B}{3x+1}.$$
Multiply by the common denominator to get
$$2 = A(3x+1) + B(3x-1).$$
Combining like-terms on the right yields
$$2 = (3A+3B)x + (A-B).$$
Noting that the "coefficient of $x$" on the left is zero, we equate coefficients to get the following system of two linear equations in two variables ($A$ and $B$):
$$\left\{ \begin{array}{lll}
3A+3B &= 0 & (i) \\
A-B &= 2 & (ii).
\end{array} \right.$$
By $(ii)$ we conclude that $A=2+B$. Plug this into $(i)$ to get
$$3(2+B)+3B=0,$$
or equivalently,
$$6B = -6,$$
i.e. $B = -1$, and hence $A=2+(-1) = 1$. This gives us the partial fractions decomposition
$$\dfrac{2}{9x^2-1} = \dfrac{1}{3x-1} - \dfrac{1}{3x+1}.$$
Therefore we may compute
$$\begin{array}{ll}
\displaystyle\int \dfrac{2}{9x^2-1} \mathrm{d}x &= \displaystyle\int \dfrac{1}{3x-1} \mathrm{d}x - \displaystyle\int \dfrac{1}{3x+1} \mathrm{d}x \\
&\stackrel{u=3x-1,v=3x+1}{=} \dfrac{1}{3} \displaystyle\int \dfrac{1}{u} \mathrm{d}u - \dfrac{1}{3} \displaystyle\int \dfrac{1}{v} \mathrm{d}v \\
&= \dfrac{1}{3} \log(u) - \dfrac{1}{3} \log(v) + C \\
&= \dfrac{1}{3} \log(3x-1) - \dfrac{1}{3} \log(3x+1) + C.
\end{array}$$
Section 8.5 #9: $$\displaystyle\int \dfrac{x^2+12x+12}{x^3-4x} \mathrm{d}x$$
Solution: We may factor this denominator as
$$x^3-4x = x(x^2-4) = x(x-2)(x+2),$$
so the partial fractions decomposition involves three terms (one for each linear factor):
$$\dfrac{x^2+12x+12}{x^3-4x} = \dfrac{A}{x} + \dfrac{B}{x-2} + \dfrac{C}{x+2}.$$
Multiplying by the common denominator $x(x-2)(x+2)$ yields
$$x^2+12x+12 = A(x-2)(x+2) + Bx(x+2) + Cx(x-2)=A(x^2-4) + B(x^2+2x) + C(x^2-2x).$$
Combining like-terms yields
$$x^2+12x+12 = (A+B+C)x^2 + (2B-2C)x + (-4A).$$
Equating coefficients yields the following system of three linear equations in three variables:
$$\left\{ \begin{array}{lll}
A+B+C &= 1 & (i) \\
2B-2C &= 12 & (ii) \\
-4A &= 12 & (iii).
\end{array} \right.$$
From $(iii)$, we may conclude that $A=-3$. From $(ii)$, we may conclude that $B-C=6$, and hence $B=6+C$. Plugging $A=-3$ and $B=6+C$ into $(i)$, we get
$$-3+(6+C)+C=1,$$
from which we may conclude $C=-1$ and $B=6+(-1)=5$, yielding the partial fractions decomposition
$$\dfrac{x^2+12x+12}{x^3-4x} = -\dfrac{3}{x} + \dfrac{5}{x-2} - \dfrac{1}{x+2}.$$
Therefore we may compute
$$\begin{array}{ll}
\displaystyle\int \dfrac{x^2+12x+12}{x^3-4x} \mathrm{d}x &= -\displaystyle\int \dfrac{3}{x} \mathrm{d}x + 5 \displaystyle\int \dfrac{1}{x-2} \mathrm{d}x - \displaystyle\int \dfrac{1}{x+2} \mathrm{d}x \\
&= -3\log(x) + 5 \log(x-2) - \log(x+2) + C.
\end{array}$$
Section 8.5 #13: $$\displaystyle\int \dfrac{4x^2+2x-1}{x^3+x^2} \mathrm{d}x$$
Solution: Factoring the denominator yields
$$x^3+x^2 = x^2(x+1).$$
Therefore we set up the partial fraction equation:
$$\dfrac{4x^2+2x-1}{x^3+x^2} = \dfrac{A}{x} + \dfrac{B}{x^2} + \dfrac{C}{x+1}.$$
This yields a system of three equations in three variables and hence the following partial fractions decomposition:
$$\dfrac{4x^2+2x-1}{x^3+x^2} = -\dfrac{1}{x^2} + \dfrac{1}{x+1} + \dfrac{3}{x}.$$
Therefore we compute
$$\begin{array}{ll}
\displaystyle\int \dfrac{4x^2+2x-1}{x^3+x^2} \mathrm{d}x &= -\displaystyle\int x^{-2} \mathrm{d}x + \displaystyle\int \dfrac{1}{x+1} \mathrm{d}x + 3 \displaystyle\int \dfrac{1}{x} \mathrm{d}x \\
&= \dfrac{1}{x} + \log(x+1) + 3\log(x) + C.
\end{array}$$

