.
Back to the class
Section 7.1 #6: Set up the definite integral that gives the area in the region bounded by $y_1=(x-1)^3$ and $y_2=x-1$:
Solution: First draw the region:
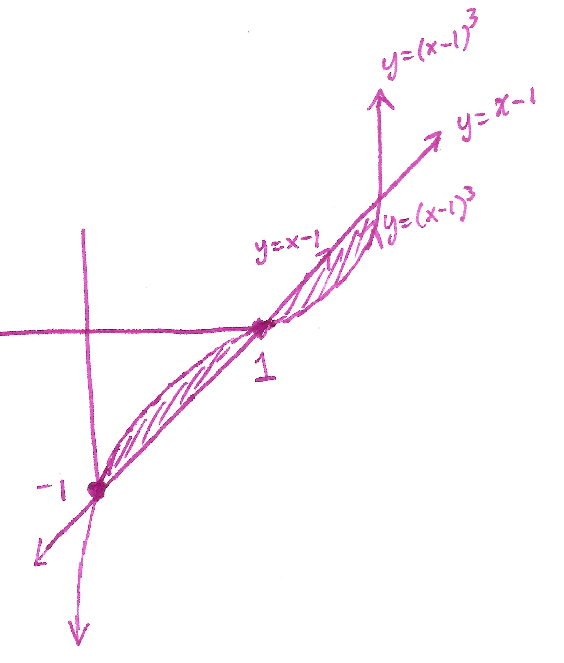
We will use a $\mathrm{d}x$ integral. It will require two such integrals. For the left region, the function on top is $y_1$ and the function on the bottom is $y_2$ and in the right region, the function on top is $y_2$ and the function on the bottom is $y_1$. Therefore we may compute the area with
$$\mathrm{Area}=\mathrm{LeftArea}+\mathrm{RightArea}=\displaystyle\int_0^1 (x-1)^3 - (x-1) \mathrm{d}x + \displaystyle\int_1^2 (x-1) - (x-1)^3 \mathrm{d}x.$$
Section 7.1 #16: Find the area of the region bounded by $y=x^2$ and $y=6-x$ by integrating...
a.) with respect to $x$, and
b.) with respect to $y$.
c.) Compare your results. Which was simpler?
Solution: First draw the region:
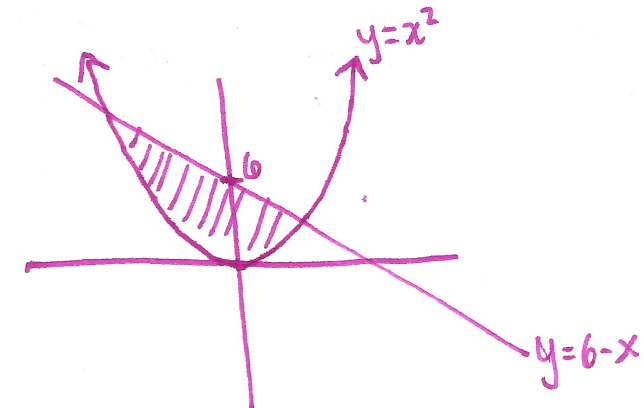
For a.), the top function is always the linear function and the bottom function is the quadratic. Therefore the area is given by
$$\begin{array}{ll}
\mathrm{Area}&=\displaystyle\int_{-3}^2 (6-x) - x^2 \mathrm{d}x \\
&= 6x - \dfrac{x^2}{2} - \dfrac{x^3}{3} \Bigg|_{-3}^2 \\
&= \left( 12 - \dfrac{4}{2} - \dfrac{8}{3} \right) - \left( -18 - \dfrac{9}{2} + \dfrac{27}{3} \right) \\
&= \dfrac{125}{6}.
\end{array}$$
For b.), the right and left functions change at $(2,4)$. First rewrite $y=x^2$ as $x=\pm \sqrt{y}$ and rewrite $y=6-x$ as $x=6-y$. Between $y=0$ and $y=4$, the function $x=\sqrt{y}$ is on the right and the function $x=-\sqrt{y}$ is on the left. Between $y=4$ and $y=9$, the function $x=6-y$ is on the right and the function $x=-\sqrt{y}$ is on the left. Therefore,
$$\begin{array}{ll}
\mathrm{Area} &= \displaystyle\int_0^4 \sqrt{y} - (-\sqrt{y}) \mathrm{d}y + \displaystyle\int_4^9 (6-y) - (-\sqrt{y}) \mathrm{d}y \\
&=2\displaystyle\int_0^4 y^{\frac{1}{2}} \mathrm{d}y + \displaystyle\int_4^9 6-y+y^{\frac{1}{2}} \mathrm{d}y \\
&= 2 \left[ \dfrac{y^{\frac{3}{2}}}{\frac{3}{2}} \right|_0^4 + \left[ 6y - \dfrac{y^2}{2} + \dfrac{y^{\frac{3}{2}}}{\frac{3}{2}} \right|_4^9 \\
&=\dfrac{4}{3} \left[ 4^{\frac{3}{2}} - 0 \right] + \left[ \left(54 - \dfrac{81}{2} + \dfrac{2}{3}9^{\frac{3}{2}} \right) - \left( 24 - \dfrac{16}{2} + \dfrac{2}{3} 4^{\frac{3}{2}} \right)\right] \\
&= \dfrac{32}{3} + \left[ \dfrac{63}{2} - \dfrac{64}{3} \right] \\
&= \dfrac{125}{6}.
\end{array}$$
For c.), we got the same result both ways and the $\mathrm{d}x$ integral was much simpler!
Section 7.1 #17: Sketch the region bounded by the graphs of the equations and find the area of region: $y=x^2-1$, $y=-x+2$, $x=0$, and $x=1$.
Solution: First find intersection points of the first two curves by setting them equal and solving:
$$x^2-1 = -x+2,$$
which is algebraically equivalent to
$$x^2+x-3=0.$$
Solving this equation (using the quadratic formula) yields the roots
$$x= \dfrac{-1 \pm \sqrt{1^2-4(1)(3)}}{2} = -\dfrac{1}{2} \pm \dfrac{\sqrt{13}}{2}.$$
Now sketch the region:
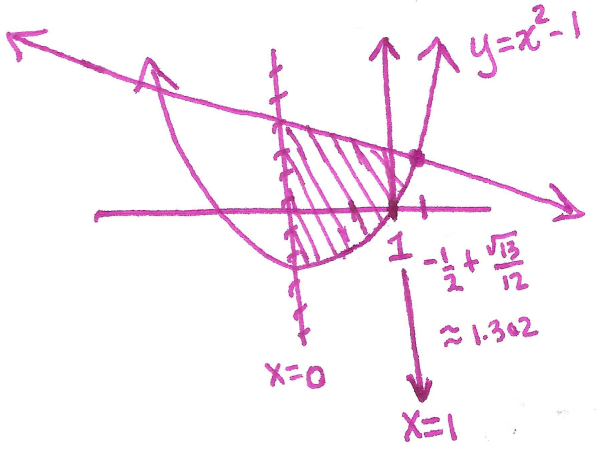
It is easier to do this as a $\mathrm{d}x$ integral: compute
$$\begin{array}{ll}
\mathrm{Area} &= \displaystyle\int_0^1 (-x+2) - (x^2-1) \mathrm{d}x \\
&= \displaystyle\int_0^1 -x^2-x+3 \mathrm{d}x \\
&= \left. -\dfrac{x^3}{3} - \dfrac{x^2}{2} + 3x \right|_0^1 \\
&= \left( - \dfrac{1}{3} - \dfrac{1}{2} + 3 \right) - 0 \\
&= \dfrac{13}{6}.
\end{array}$$
Section 7.1 #21: Sketch the region bounded by the graphs of the equations and find the area of region: $y=x$, $y=2-x$, $y=0$.
Solution: First find the intersection points between $y=x$ and $y=2-x$ by setting them equal:
$$x=2-x,$$
hence
$$x=1.$$
Therefore $(1,1)$ is the intersection point of the two curves. Now sketch the region:
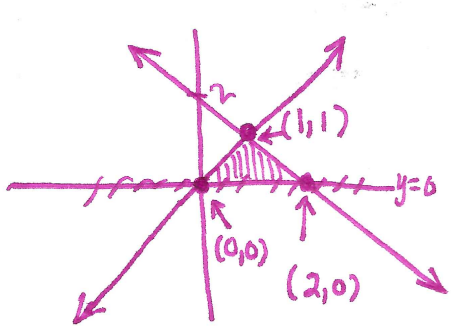
It is easier to do this integral as a $\mathrm{d}y$ (notice that if we did a $\mathrm{d}x$, then it would require two integrals). The "right" function is $x=2-y$ and the "left" function is $x=y$. Therefore we compute
$$\begin{array}{ll}
\mathrm{Area} &= \displaystyle\int_0^1 (2-y) - y \mathrm{d}y \\
&=\displaystyle\int_0^1 2-2y \mathrm{d}y \\
&=2y - y^2 \Bigg|_0^1 \\
&= (2-1) - 0 \\
&= 1.
\end{array}$$
Section 7.2 #22: Sketch the region bounded by the graphs of the equations and find the area of region: $y=\dfrac{4}{x^3}$, $y=0$, $x=1$, and $x=4$.
Solution: Sketch the region:
This is easier to do as a $\mathrm{d}x$ integral, so compute
$$\begin{array}{ll}
\displaystyle\int_1^4 \dfrac{4}{x^3} \mathrm{d}x &= 4 \displaystyle\int_1^4 x^{-3} \mathrm{d}x \\
&= -\dfrac{4}{2} x^{-2} \Bigg|_1^4 \\
&= -\dfrac{4}{2} \dfrac{1}{4^2} + \dfrac{4}{2} \dfrac{1}{1} \\
&= 2 - \dfrac{1}{8} \\
&= \dfrac{15}{8}.
\end{array}$$
