Back to the class
Section 2.4 #17: Determine whether the graph of the equation $3x^2-2y^2=3$ is symmetric with respect to the $x$-axis, the $y$-axis, and/or the origin.
Solution:
test for symmetry with respect to $x$-axis: Replace $y$ with $-y$ to get the equation
$$3x^2 - 2(-y)^2 = 3.$$
Since $(-y)^2 = (-y)(-y) = y^2$ this equation is equivalent to
$$3x^2 - 2y^2 = 3.$$
This equation is the same as the original, so the grpah is symmetric with respect to the $x$-axis.
test for symmetry with respect to $y$-axis: Replace $x$ with $-x$ to get the equation
$$3(-x)^2-2y^2=3.$$
Since $(-x)^2=x^2$, this equation is equivalent to
$$3x^2-2y^2=3,$$
which is the same as the original. Hence the graph is symmetric with respect to the $y$-axis.
test for symmetry with respect to origin Replace $x$ with $-x$ and $y$ with $-y$ to get
$$3(-x)^2-2(-y)^2=3.$$
Since $(-x)^2=x^2$ and $(-y)^2=y^2$ this is equivalent to
$$3x^2-2y^2=3,$$
which is the original equation. Hence the graph is symmetric with respect to the origin.
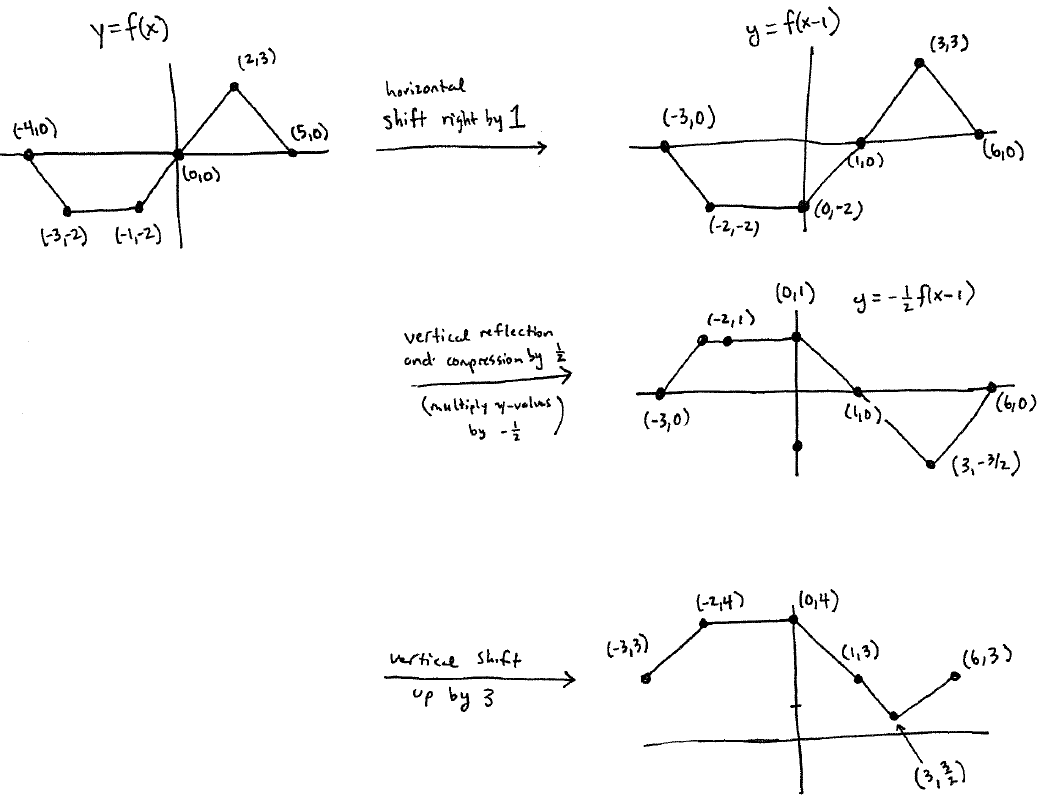
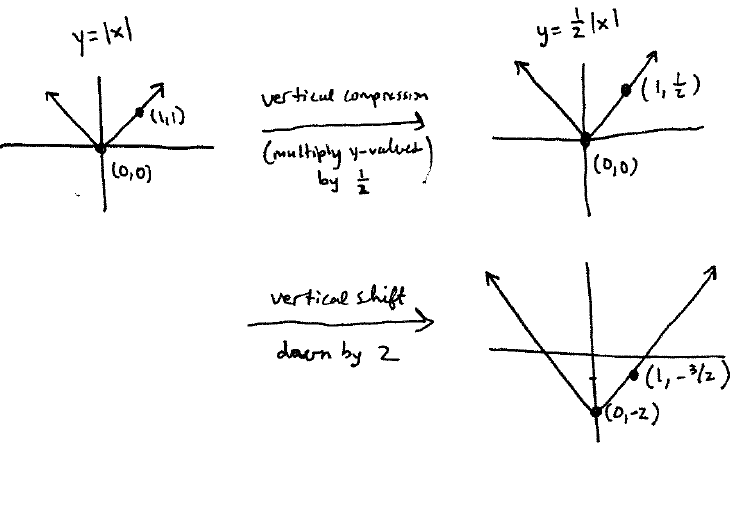
Section 2.5 #11: Describe how the graph of $f(x)=\dfrac{1}{2}|x|-2$ can be obtained and graph it.
Solution: We start with the graph of $y=|x|$. We then apply a vertical stretch of $\dfrac{1}{2}$ (by multiplying $y$-value by $\dfrac{1}{2}$). After that we apply a vertical shift down by $2$ (i.e. subtract $2$ from each $y$-value).
Section 2.5 #37: The point $(-12,4)$ is on the graph of $y=f(x)$. Find the corresponding point on the graph of $y=g(x)$ where $g(x)=\dfrac{1}{2}f(x)$.
Solution: The factor of $\dfrac{1}{2}$ tells us there is a vertical compression by a factor of $\dfrac{1}{2}$, meaning that we multiply $y$-values by $\dfrac{1}{2}$. Doing so to the point $(-12,4)$ yields the point $(-12,2)$.
Section 2.5 #50: Write an equation for a function that has a graph with the following characteristics: the shape of $y=\sqrt{x}$, but shifted left $6$ units and down $5$ units.
Solution: Start with $y=\sqrt{x}$. Shifting it left by $6$ would give us $y=\sqrt{x+6}$. Shifting that down by $5$ units gives us $y=\sqrt{x+6}-5$.
Section 2.5 #63: The graph of $y=f(x)$ is given as follows:
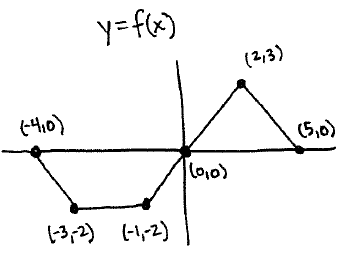
Now graph $y=g(x)$ where $g(x)=-\dfrac{1}{2} f(x-1)+3$.
Solution: