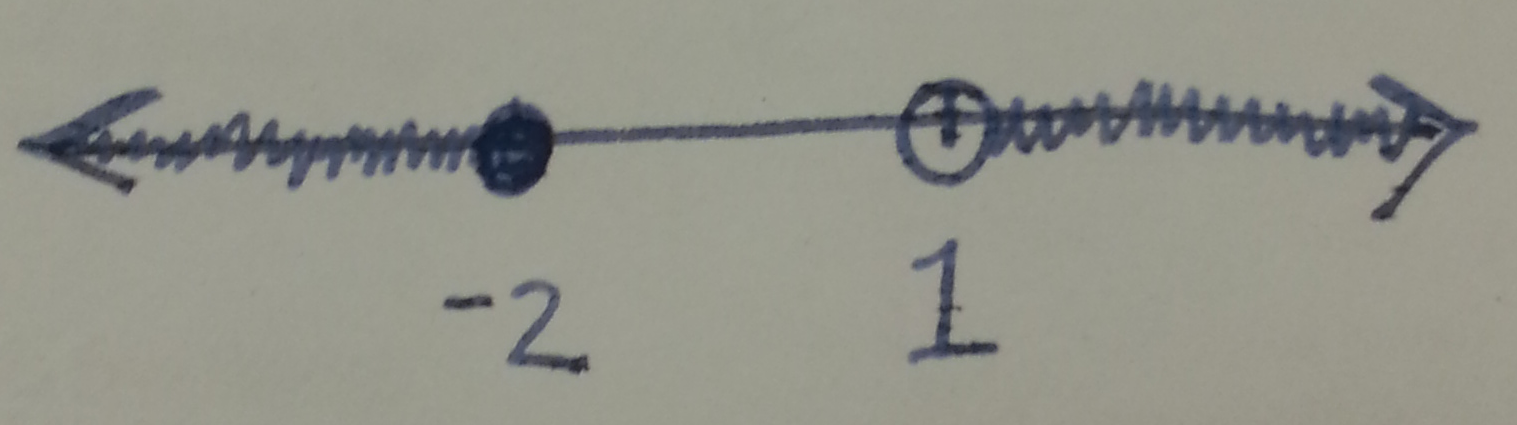Back to the class
Section 1.4 #19: Find an equation of the line that passes through the points $\left( -1, 5 \right)$ and $\left(2 , -4 \right)$.
Solution: We will first find its slope and the use the point-slope form of the line. The slope is
$$m=\dfrac{-4-5}{2-(-1)}=\dfrac{-9}{3} = -3.$$
Using the point-slope form of the equation of the line with slope $m=-3$ and the point $(x_1,y_1)=(-1,5)$ we get
$$y-5 = -3(x-(-1))$$
or
$$y-5 = -3(x+1),$$
or the slope-intercept form
$$y=-3x+2.$$
Section 1.4 #43: Find an equation of the line passing through $(3,5)$ parallel to and perpendicular to the line $y=\dfrac{2}{7}x+1$.
Solution: Since the slope of the given line is $\dfrac{2}{7}$ the slope of the line parallel is also $\dfrac{2}{7}$. Therefore using the point-slope form we get the following equation for the parallel line:
$$y-5 = \dfrac{2}{7}(x-3),$$
or in slope-intercept form
$$y=\dfrac{2}{7}x+\dfrac{29}{7}.$$
Since the slope of the given line is $\dfrac{2}{7}$ the slope of the line parallel is $-\dfrac{7}{2}$. Therefore using the point-slope form we get the following equation for the perpendicular line:
$$y-5 = -\dfrac{7}{2}(x-3),$$
or in slope-intercept form
$$y=-\dfrac{7}{2}x + \dfrac{31}{2}.$$
Section 1.5 #36: Khalid makes an investment at $4\%$ simple interest. At the end of $1$ year, the total value of the investment is $\$1560$. How much was originally invested?
Solution: Recall the formula $I=Prt$. We are told in the problem that $t=1$ and $r=0.04$. We seek $P$ but we are not told $I$. We are told the value of $P+I=1560$ (note: interest is just the extra that accrues but we are told the total value after $1$ year). Therefore in the equation $I=Prt$ we may replace $I$ with $1560-P$ and substitute our other values to get
$$1560-P=P(0.04)(1).$$
Add $P$ to both sides to get
$$1560 = 1.04 P.$$
Hence the amount originally invested is
$$P = \dfrac{1560}{1.04} = 1500.$$
Section 1.5 #37: In triangle $ABC$, angle $B$ is five times as large as angle $A$. The measure of angle $C$ is $2^{\circ}$ less than that of angle $A$. Find the measures of the angles.
Solution: We add the three angles and use the fact that sum of the angles in a triangle is $180$ to get
$$5x+x+(x-2)=180.$$
Simplify the left-hand isde to get
$$7x = 182,$$
or and solve for the value of angle $A$:
$$x=\dfrac{182}{7}=26.$$
Therefore angle $B$ is $26 \cdot 5 = 130$ and angle $C$ is $26-2=24$.
Section 1.6 #35: Solve and graph the inequality
$$3x \leq -6 \hspace{2pt} \mathrm{or} \hspace{2pt} x-1>0.$$
Solution: Divide the left piece $3x \leq -6$ by $3$ to get
$$x \leq -2.$$
Add $1$ to the right piece to get $x>1$. Now we graph both inequalities simultaneously: