Back to the class
Section 1.2 #56: Find the domain of the function $f(x)=\dfrac{8}{x+4}$.
Solution: The domain of this function can be found by considering where the denominator equals zero. So we require the denominator to be nonzero, i.e. $x+4 \neq 0$. Isolating $x$ shows us that $x \neq -4$. Therefore the domain of $f$ is $\mathbb{R} \setminus \{-4\}$ (or written as $(-\infty,-4) \cup (-4,\infty)$ or written as $\{x \colon x \mathrm{\hspace{2pt} is \hspace{2pt} a \hspace{2pt} real \hspace{2pt} number \hspace{2pt} and \hspace{2pt}} x \neq -4\}$ or written as "all real numbers except $x=-4$" or written as "$-\infty < x < -4$ or $-4 < x < \infty$").
Section 1.2 #66: Find the domain and range of the function whose graph is pictured:
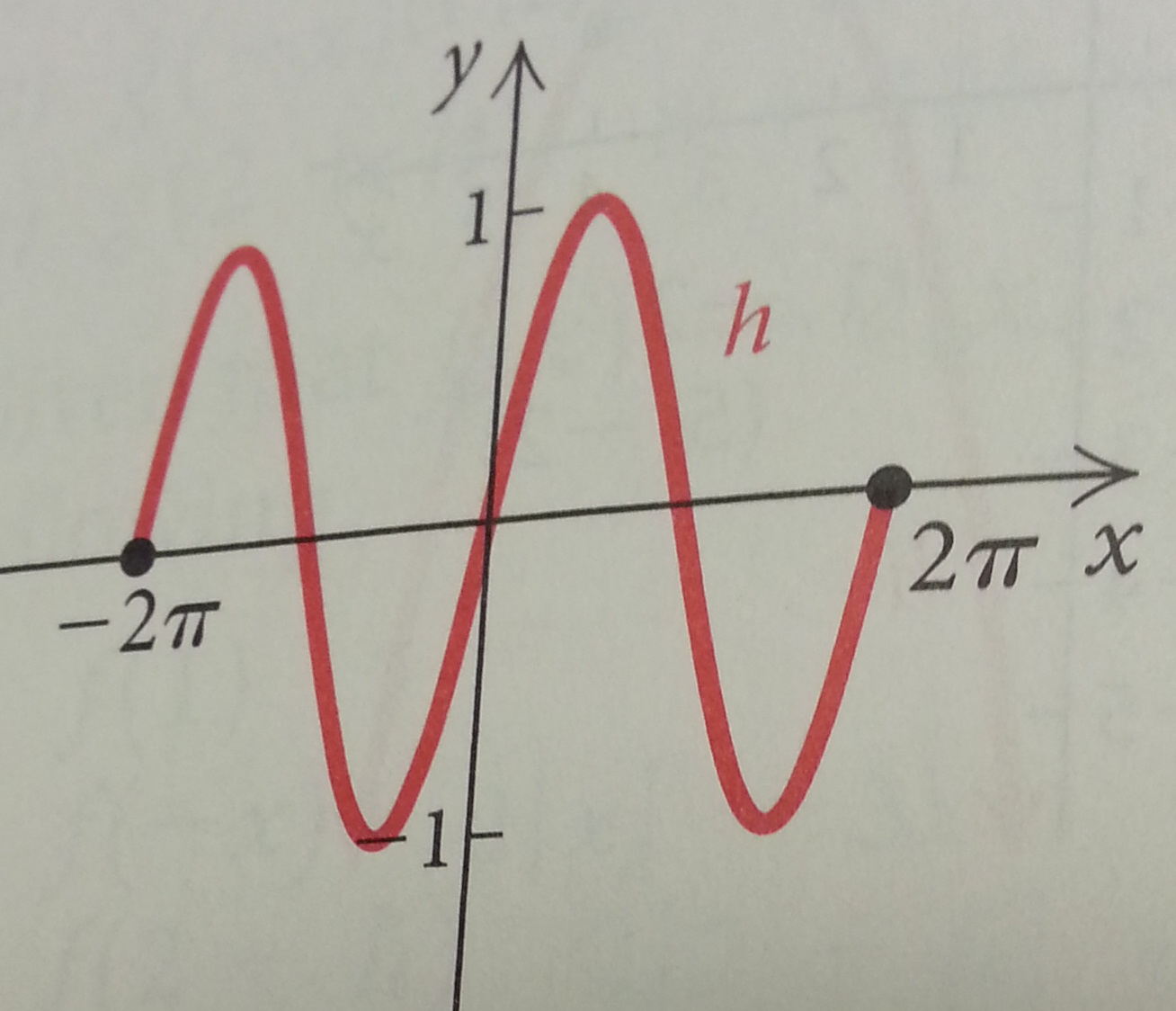
Solution: The domain is the set of inputs which have an output. That means we are looking for where on the $x$-axis has a point shaded in above or below it, i.e. the interval $[-2\pi,2\pi]$. You may also write this domain in the following ways: $2\pi \leq x \leq 2\pi$ or "all real numbers between $-2\pi$ and $2\pi$, including both $-2\pi$ and $2\pi$".
The range is the set of numbers which are actually outputted by the function. To find it, look up and down the $y$-axis for the places which have a shaded dot to the left or right of the $y$-axis -- i.e. $[-1,1]$.
Section 1.3 #6: Find the slope of the line containing the points $(-3,1)$ and $(3,-5)$.
Solution: Recall the slope of the line containing the points $(x_1,y_1)$ and $(x_2,y_2)$ is $\mathrm{slope}=m=\dfrac{y_2-y_1}{x_2-x_1}$. Therefore we compute
$$\mathrm{slope}=m=\dfrac{-5-1}{3-(-3)} = \dfrac{-6}{6}=-1.$$
Section 1.3 #32: Find the slope of the graph of the linear equation $y=-\dfrac{2}{5}x+7$.
Solution: This equation is already in slope-intercept form. Therefore we may "read off" the slope as the coefficient of $x$, i.e. the slope is $-\dfrac{2}{5}$.
Section 1.3 #55: Find the slope and the $y$-intercept of the line with equation $3x+2y=10$.
Solution: This equation is not in "slope-intercept" form, so it is not as straightforward as #32 to answer the question. One way to proceed is to algebraically manipulate the equation into slope-intercept form: start with
$$3x+2y=10,$$
subtract $3x$ from both sides to get
$$2y = -3x+10,$$
divide both sides by $2$ to get
$$y = -\dfrac{3}{2}x+5.$$
This equation is equivalent to the original and is in slope-intercept form. Therefore we see the slope is $-\dfrac{3}{2}$ and the $y$-intercept is $(0,5)$. (note: if you ask WolframAlpha to find the y-intercept, it only reports "5" -- their definition of y-intercept is not as a point like ours is...be careful!)

