Return to the class
Homework 3
Section 7.3 #20: Find the exact value of $\cos(0)$.
Solution: In the unit circle, the point that goes with angle $0$ radians is $(1,0)$. Since the cosine reads the $x$-coordinate of points on the unit circle, we must conclude that $\cos(0)=1$.
Section 7.3 #21: Find the exact value of $\cos \left( \dfrac{\pi}{6} \right)$.
Solution: In the unit circle, the point that goes with angle $\dfrac{\pi}{6}$ radians is $\left( \dfrac{\sqrt{3}}{2}, \dfrac{1}{2} \right)$. Since the cosine reads the $x$-coordinate of points on the unit cicle, we must conclude that $\cos \left( \dfrac{\pi}{6} \right)=\dfrac{\sqrt{3}}{2}$.
Section 7.3 #24: Find the reference angle for the angle $-170^{\circ}$.
Solution: The angle is in quadrant III, since it is less than $-90^{\circ}$ but greater than $-180^{\circ}$. Let us first express this negative angle as a posistive angle: to do that recall that a full rotation is $360^{\circ}$, so adding a full rotation yields the same terminal side of the angle (and hence the same angle -- remember that an angle is merely a pair of rays, by definition). So
$$-170^{\circ} \stackrel{\mathrm{as \hspace{2pt} angles}}{=} -170^{\circ}+360^{\circ}=190^{\circ}.$$
To find the reference angle, we note that all angles in quadrant III have a reference angle given by subtracting half a rotation, i.e.
$$\mathrm{ref \hspace{2pt} angle}=190^{\circ}-180^{\circ}=10^{\circ}.$$
Section 7.3 #29: Find the reference angle for the angle $\dfrac{2\pi}{3}$.
Solution: This angle lies in quadrant II and so its reference angle is given by
$$\mathrm{reference \hspace{2pt} angle}=\pi - \dfrac{2\pi}{3} = \dfrac{\pi}{3}.$$
Section 7.3 #44: Find the reference angle, the quadrant of the terminal side, and the sine and cosine of $\dfrac{5\pi}{3}$.
Solution: The angle $\dfrac{5\pi}{3}$ lies in quadrant IV. To see this for sure, let us compare to the angle $\dfrac{3\pi}{2}$ (which is the angle that separates quadrant III and quadrant IV) and to the angle $2\pi$. To compare them, we need a common denominator: $6$. So rewrite $\dfrac{5\pi}{3}=\dfrac{10\pi}{6}$, $\dfrac{3\pi}{2}=\dfrac{9\pi}{6}$, and $2\pi = \dfrac{12\pi}{6}$. Sice $9 < 10 < 12$, it follows that $\dfrac{9\pi}{6} < \dfrac{10\pi}{6} < \dfrac{12\pi}{6}$, in other words, $\dfrac{3\pi}{2} < \dfrac{5\pi}{3} < 2\pi$. This shows that $\dfrac{5\pi}{3}$ is in quadrant IV.
Since it is in quadrant IV, its reference angle is $2\pi-\dfrac{5\pi}{3}=\dfrac{6\pi}{3}-\dfrac{5\pi}{3}=\dfrac{\pi}{3}$. From this we know that the sine of $\dfrac{5\pi}{3}$ must be negative and the cosine of $\dfrac{5\pi}{3}$ must be positive, hence
$$\sin \left( \dfrac{5\pi}{3} \right) = -\sin \left( \dfrac{\pi}{3} \right)=-\dfrac{\sqrt{3}}{2},$$
and
$$\cos \left( \dfrac{5\pi}{3} \right) = +\cos \left(\dfrac{\pi}{3} \right) = \dfrac{1}{2}.$$
Section 7.3 #53: If $\sin(t)=-\dfrac{1}{4}$ and $t$ is in the third quadrant, find $\cos(t)$.
Solution: Since $t$ is in the third quadrant, we must conclude that $\cos(t)$ is negative. Since $\sin(t)=-\dfrac{1}{4}$, this means that the $y$-coordinate of the point associated with the angle $t$ is $-\dfrac{1}{4}$. To find the cosine of $t$ means to find the $x$-coordinate corresponding to this $y$-coordinate. To do that recall that the unit circle obeys the formula $x^2+y^2=1$, and we are told that $y=-\dfrac{1}{4}$. Plugging that value in yields
$$x^2 + \left( -\dfrac{1}{4} \right)^2 = 1.$$
In other words, $x^2+\dfrac{1}{16}=1$, so $x = \pm \sqrt{ \dfrac{15}{16} }= \pm\dfrac{\sqrt{15}}{4}$. But since $t$ is in quadrant III, we must take the negative solution. Therefore we see that
$$\cos(t) = -\dfrac{\sqrt{15}}{4}.$$
Section 7.3 #71: In the following picture, find the value of the sine and the cosine at $t$:
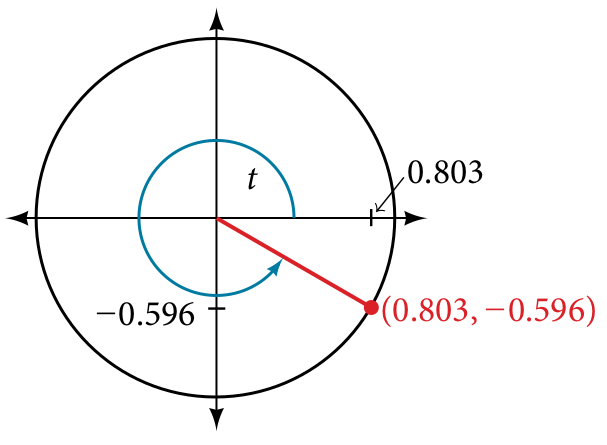
Solution: Since sine is the $y$-coordinate and cosine is the $x$-coordinte, we see
$$\sin(t)=-0.5966,$$
and
$$\cos(t)=0.803.$$
Section 7.3 #87: Use a calculator to evaluate $\cos \left( 98^{\circ} \right)$.
Solution: Calculate (make sure the calculator is in degree mode)
$$\cos \left( 98^{\circ} \right) \approx -0.13917.$$
Section 7.3 #88: Use a calculator to evaluate $\cos(310^{\circ})$.
Solution: Calculate (make sure the calculator is in degree mode)
$$\cos(310^{\circ})\approx 0.64278.$$



