Back to the class
Section 7.4: #21: Consider $y=\sin(x)$ on $0 \leq x \leq \pi$:
a.) Sketch the graph of the function.
b.) Find a definite integral that represents the arc length of the curve over the indicated interval.
Solution: For part a.),
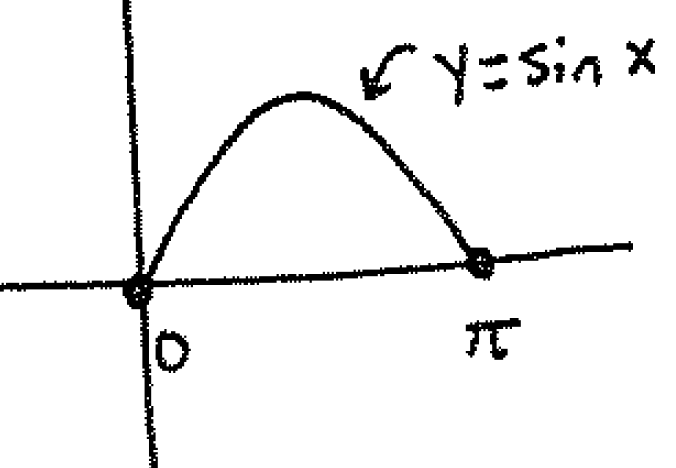
Note that $\dfrac{\mathrm{d}}{\mathrm{d}x} \sin(x)=\cos(x)$. Therefore, the arc length of the curve is
$$\mathrm{arclength}=\displaystyle\int_0^{\pi} \sqrt{1+\cos^2(x)} \mathrm{d}x.$$
Section 7.4: #44: Find the surface area of the surface generated by revolving the curve $y=9-x^2$ $0 \leq x \leq 3$ about the $y$-axis.
Solution: The described region is
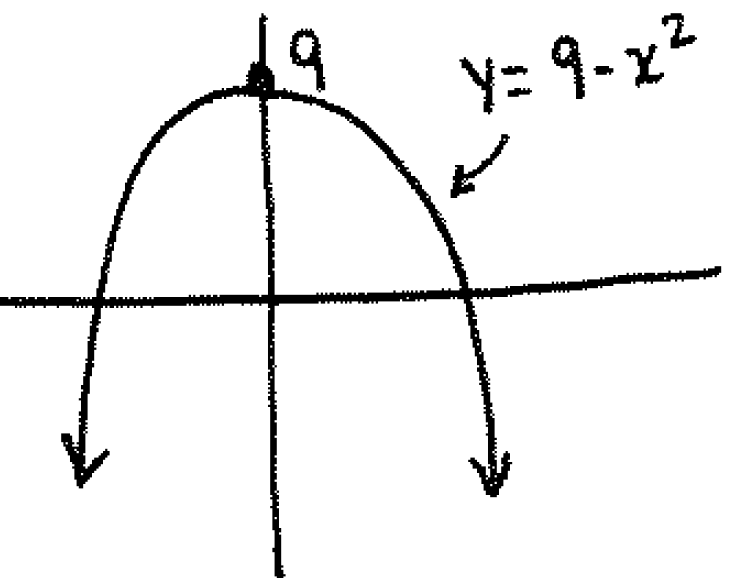
and so we rotate it about the $y$-axis as follows:
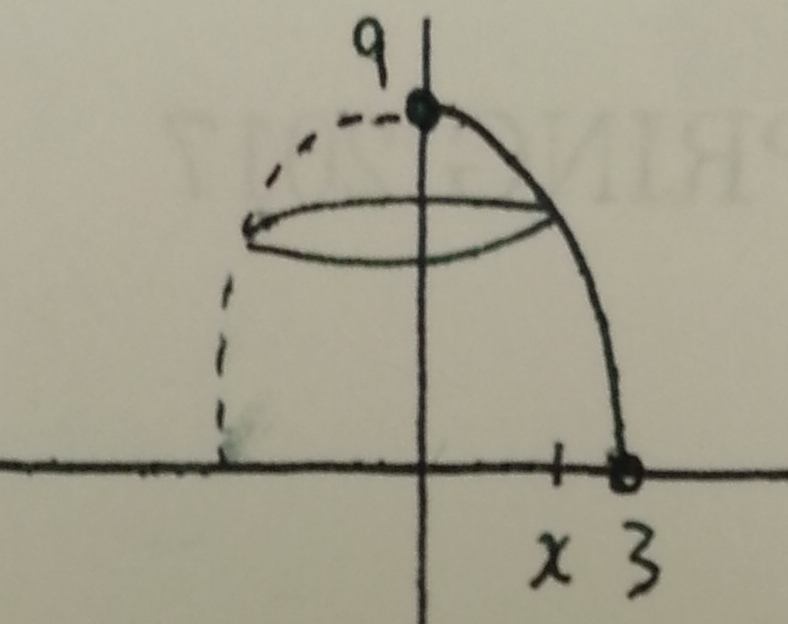
Note the derivative $\dfrac{\mathrm{d}}{\mathrm{d}x}[9-x^2]=-2x$. Therefore we see that
$$\begin{array}{ll}
\mathrm{SurfaceArea} &= 2\pi \displaystyle\int_0^3 x \sqrt{1+(-2x)^2} \mathrm{d}x \\
&= 2\pi \displaystyle\int_0^3 x \sqrt{1+4x^2} \mathrm{d}x \\
&\stackrel{u=1+4x^2}{=} \dfrac{2\pi}{8} \displaystyle\int_1^{37} u^{\frac{1}{2}} \mathrm{d}u \\
&=\dfrac{\pi}{4} \left[ \dfrac{2}{3} u^{\frac{3}{2}} \right|_1^{37} \\
&=\dfrac{\pi}{6} \left[ 37^{\frac{3}{2}} - 1 \right]
\end{array}$$
Section 10.2 #3: Sketch the curve represented by the parametric equtions and write the corresponding rectangular equation by eliminating the parameter:
$$\left\{ \begin{array}{ll}
x(t)=t+1 \\
y(t)=t^2\\
\end{array} \right.$$
Solution: First sketch the parametric curve:
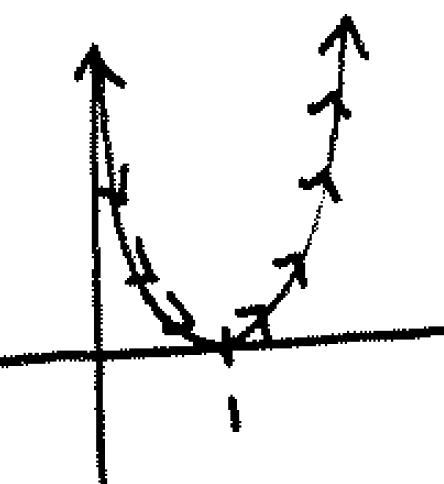
To eliminate parameters, write $x=t+1$ as $t=x-1$ and write $y=t^2$ as $t = \pm \sqrt{y}$ (but we take only $t=\sqrt{y}$ because our graph only has positive $y$-values). Set these equal and we get $x-1=\sqrt{y}$, or in other words (squaring both sides) $y=(x-1)^2$ (either answer will suffice for credit).
Section 10.3 #20: Consider the parametric equations
$$\left\{ \begin{array}{ll}
x(t) &= t-2 \\
y(t) &= \dfrac{1}{t}+3
\end{array} \right.$$
Find an equation for the tangent line of the curve at the parameter $t=1$.
Solution: We draw this:
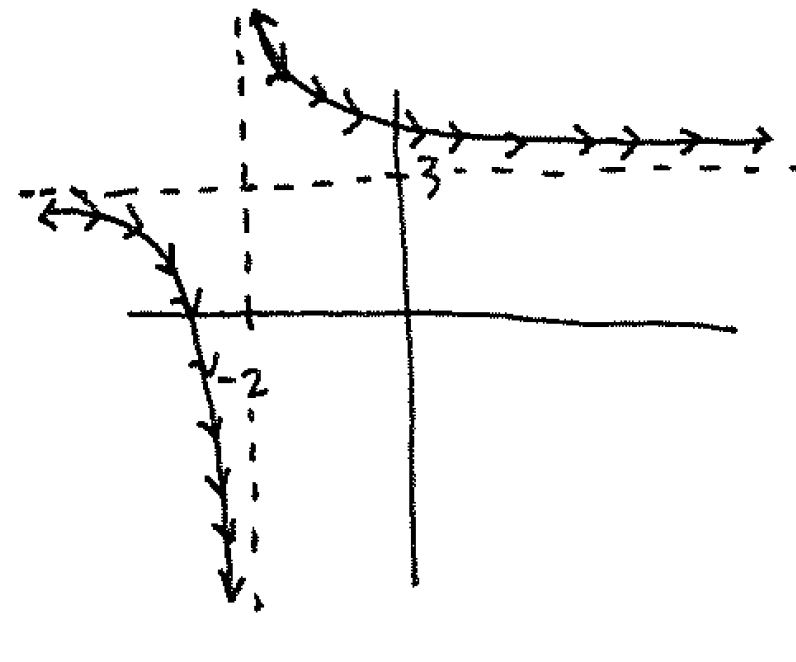
The point corresponding to the parameter $t=1$ is $(x(1),y(1))=(-1,4)$. To find the tangent line, we must figure out what $\dfrac{\mathrm{d}y}{\mathrm{d}x}=\dfrac{\frac{\mathrm{d}y}{\mathrm{d}t}}{\frac{\mathrm{d}x}{\mathrm{d}t}}$ is. Compute
$$x'(t)=1,$$
and
$$y'(t)=-\dfrac{1}{t^2}.$$
Therefore
$$\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{-\frac{1}{t^2}}{1} = -\dfrac{1}{t^2}.$$
Therefore the slope of the tangent line at $(-1,4)$ (i.e. at parameter $t=1$) is
$$\dfrac{\mathrm{d}y}{\mathrm{d}x} \Bigg|_{t=1} = -\dfrac{1}{1^2} =-1.$$
Therefore the tangent line at $(-1,4)$ is the line going through that point with slope $-1$, i.e.
$$y-4 = -1(x-(-1)),$$
or
$$y-4=-(x+1),$$
or any other equivalent form of the equation for this line.
Section 10.4 #3: Plot the given point in polar coordinates and find its corresponding rectangular coordinates: $\left( -4, -\dfrac{3\pi}{4} \right)$.
Solution: First draw:
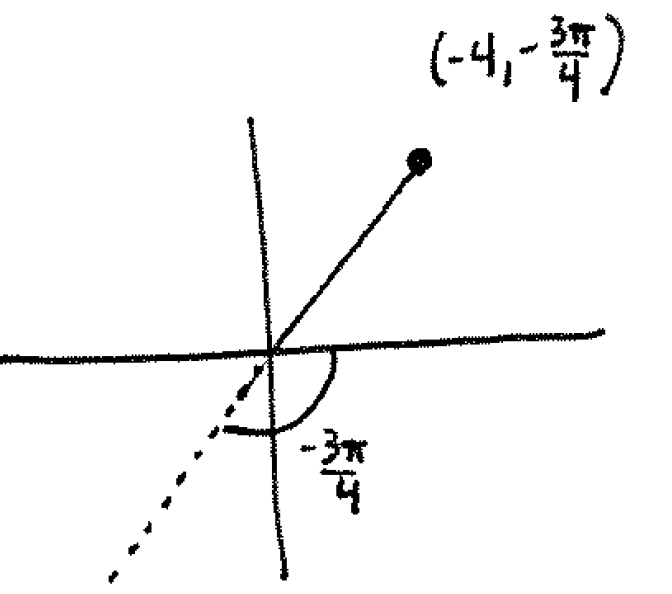
Note that since $r$ was negative, it goes "backwards". To find the rectangular coordinates, use the formulas
$$\left\{ \begin{array}{ll}
x=r\cos(\theta) \\
y=r\sin(\theta)
\end{array}\right.$$
to conclude
$$x=-4\cos \left( - \dfrac{3\pi}{4} \right) = -4 \left( - \dfrac{\sqrt{2}}{2} \right)=2\sqrt{2},$$
and
$$y=-4\sin \left( -\dfrac{3\pi}{4} \right) = -4 \left( - \dfrac{\sqrt{2}}{2} \right) = 2\sqrt{2}.$$
Therefore the rectangular coordinates of the point are $(2\sqrt{2},2\sqrt{2})$.
Section 10.4 #15: A point in rectangular coordinates is given; write this point in polar coordinates: $(-1,-\sqrt{3})$.
Solution: To find the polar coordinates, we use the formulas
$$\left\{ \begin{array}{ll}
r=\sqrt{x^2+y^2} \\
\theta = \left\{ \begin{array}{ll}
\arctan \left( \dfrac{y}{x} \right) & (x,y) \mathrm{\hspace{2pt} is \hspace{2pt} quadrants \hspace{2pt} I \hspace{2pt} or \hspace{2pt} II} \\
\pi+\arctan \left( \dfrac{y}{x} \right) & (x,y) \mathrm{\hspace{2pt} is \hspace{2pt} quadrants \hspace{2pt} III \hspace{2pt} or \hspace{2pt} IV}
\end{array} \right.
\end{array} \right.$$
For us, our point $(-1,-\sqrt{3})$ is in quadrant III, so we see that
$$r=\sqrt{(-1)^2+(-\sqrt{3})^2}=\sqrt{1+3} = \sqrt{4}=2,$$
and
$$\theta = \pi + \arctan \left( \dfrac{-\sqrt{3}}{-1} \right) = \pi + \arctan(\sqrt{3}) = \pi + \dfrac{\pi}{3}=\dfrac{4\pi}{3},$$
so we could write this point in polar coordinates as $\left( 2, \dfrac{4\pi}{3} \right)$.
Note: any angle "coterminal" with $\dfrac{4\pi}{3}$ will suffice, i.e. any angle of the form $\dfrac{4\pi}{3}+2k\pi$ will work for $k=\ldots,-2,-1,0,1,2,\ldots$








