Back to the class
Section 8.1 #24: Find a formula for the trigonometric function pictured:
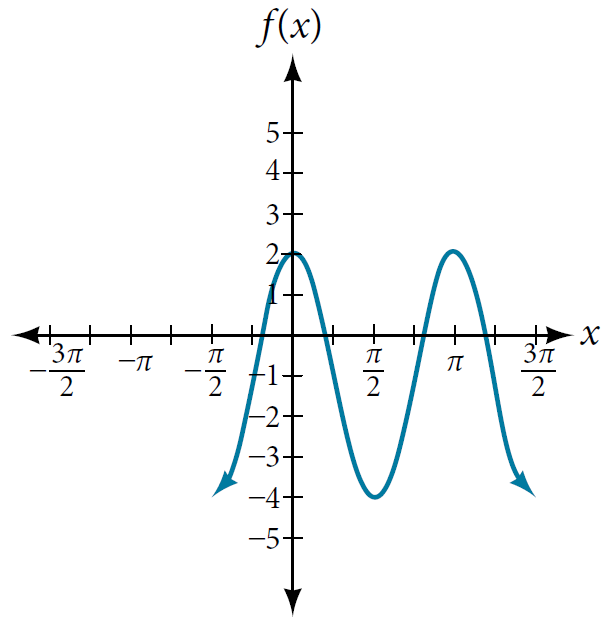
Solution: This graph is shaped like a cosine, but upside down -- this implies there is a vertical reflection. This graph oscillates between $y$-values $2$ and $-4$. The zero-line is in the middle of those values -- therefore it occurs at height $-1$. The distance between the zero line and the max height (of $2$) is $3$. This informs us that there was a vertical stretch factor of $3$ (this is called the amplitude). Normally a vertical stretch of $3$ makes the function go between $-3$ and $3$, but a vertical shift was used to alter this to go between $-4$ and $2$ -- from this we deduce that the vertical shift was $1$ down. The final anchor points in this problem (for the leftmost period) are $-\dfrac{\pi}{2}$, $-\dfrac{\pi}{4}$, $0$, $\dfrac{\pi}{4}$, and $\dfrac{\pi}{2}$. The usual anchor points for a cosine are $0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}$, and $2\pi$. Firstly, to get $4$'s in the denominators, we had to divide those "usual" anchor points by $2$ (this means there is a horizontal compression factor of $2$). That would have given us the anchor points $0, \dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3\pi}{4}$, and $\pi$. Finally, to get the anchor points in the picture, we take these and shift them left by $\dfrac{\pi}{2}$, meaning there is a horizontal shift left by $\dfrac{\pi}{2}$ after the horizontal compression was applied. Putting all of this information together yields the following function:
$$f(x)=-3\cos \left( 2 \left( x + \dfrac{\pi}{2} \right) \right)-1.$$
Section 8.2 #39: Find a formula for the trigonometric function pictured:
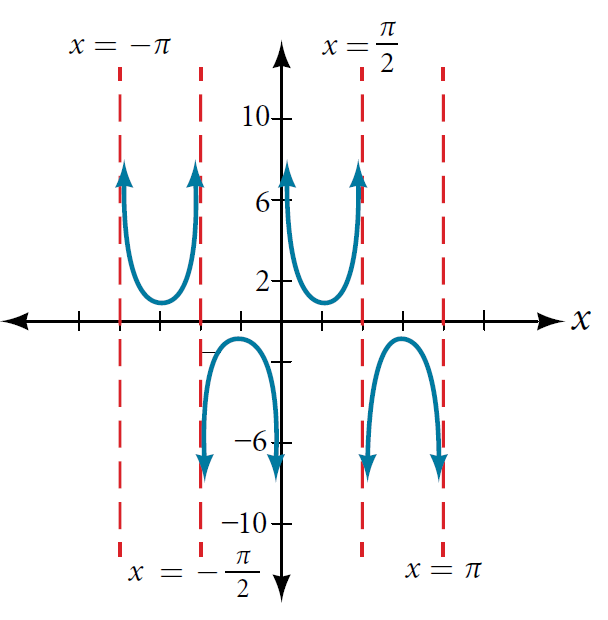
Solution: This graph is shaped like a cosecant. It appears that the anchor points being used to plot it are at $-\dfrac{\pi}{2}, -\dfrac{\pi}{4}, 0, \dfrac{\pi}{4}$, and $\dfrac{\pi}{2}$. The "usual" anchor points of cosecant are $-\pi, -\dfrac{\pi}{2}, 0, \dfrac{\pi}{2},$ and $\pi$. To get from the "usual" anchor points to the ones pictured, the "usual" anchor points were divided by $2$, meaning that there was a horizontal compression by $2$ in the function. The heights appear normal. Therefore putting the information together yields the following function:
$$f(x) = \csc(2x).$$
Section 8.2 #42: Find a formula for the trigonometric function pictured:
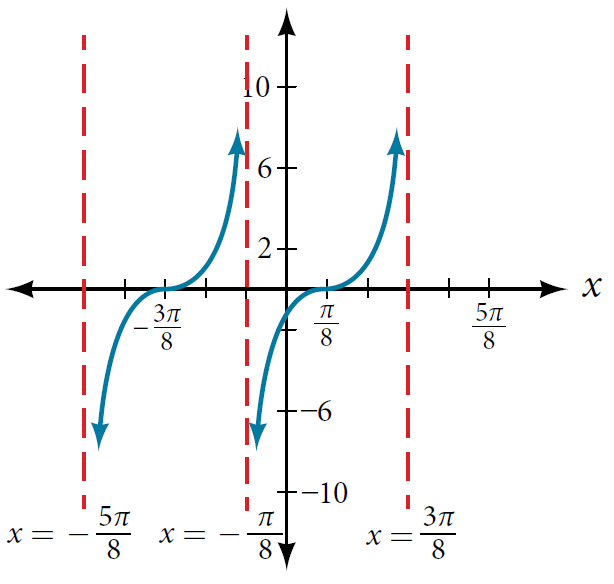
Solution:
Section 8.3 #12: Find $\tan^{-1}(1)$.
Solution: The shape of this graph is of tangent. The anchor points used to plot the second period are at $-\dfrac{\pi}{8}, 0, \dfrac{\pi}{8}, \dfrac{\pi}{4}$, and $\dfrac{3\pi}{8}$. The usual anchor points for tangent are at $-\dfrac{\pi}{2}, -\dfrac{\pi}{4}, 0 \dfrac{\pi}{4}$, and $\dfrac{\pi}{2}$. Notice we have a lot of points with denominator $8$ in the plot, so we should divide our usual anchor points by $2$, meaning there is a horizontal compression factor of $2$ (note: we don't divide by $4$ since we would end up with denominators of $16$ on some points!). Such a transformation turns the "usual" anchor points into $-\dfrac{\pi}{4}, -\dfrac{\pi}{8}, 0, \dfrac{\pi}{8}$, and $\dfrac{\pi}{4}$. Now all that must be done to shift these to the plotted anchor points is to add $\dfrac{\pi}{8}$ to each, meaning there is a horizontal shift right by $\dfrac{\pi}{8}$. The vertical values appear unaffected. Putting this information together yields the following function:
$$f(x) = \tan \left( 2 \left( x - \dfrac{\pi}{8} \right) \right).$$
Notice that the third plotted anchor point ($-\frac{\pi}{8}$) compared to the "usual" third anchor point ($0$). This suggests there is a horizontal shift left by $\dfrac{\pi}{8}$. If we apply such a shift to the "usual" anchor points we arrive at the plotted ones -- therefore the function must have such a transformation. The heights of the 2nd and 4th anchor points appear to be $2$ and $-2$ and $2$ respectively, indicating a vertical stretch by $2$. Therefore putting the information together yields the
Section 8.3 #17: Use a calculator to compute $\cos^{-1}(-0.4)$.
Solution: If the calculator is in radian mode, then compute
$$\cos^{-1}(-0.4)=1.982.$$
If the calculator is in degree mode, then compute
$$\cos^{-1}(-0.4) = 113.6^{\circ}.$$
Section 8.3 #27: Calculate $\tan^{-1} \left( \sin \left( \dfrac{\pi}{3} \right) \right)$.
Solution: Since $\sin\left( \dfrac{\pi}{3} \right)=\dfrac{\sqrt{3}}{2}$, this problem reduces to computing $\tan^{-1}\left( \dfrac{\sqrt{3}}{2} \right)$. There is no angle on the well-known points on the unit circle that answer the question "what angle has tangent equal to $\dfrac{\sqrt{3}}{2}$?", so we use a calculator and see $\tan^{-1}\left(\dfrac{\sqrt{3}}{2} \right)=0.7137$.
Section 8.3 #38: Find an exact value of $\sin(\cos^{-1}(1-x))$.
Solution: Let $\theta=\cos^{-1}(1-x)$. Then $\cos(\theta)=1-x$. Drawing a triangle for this yields the following picture:
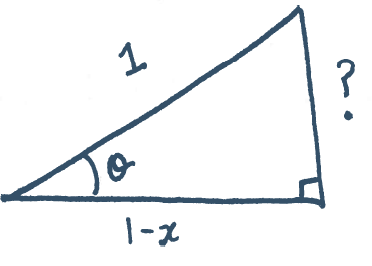To find the missing side labelled $?$, us the Pythagorean Theorem to write
$$(1-x)^2 + ?^2 = 1^2.$$
Solving for $?$ yields
$$? = \sqrt{1-(1-x)^2}.$$
Therefore compute
$$\sin(\cos^{-1}(1-x))=\sin(\theta)=\dfrac{\sqrt{1-(1-x)^2}}{1}=\sqrt{1-(1-x)^2}.$$
Section 8.3 #39: Find an exact value of $\cos \left( \sin^{-1} \left( \dfrac{1}{x} \right) \right)$.
Solution: Let $\theta=\sin^{-1}\left(\dfrac{1}{x}\right)$ so that $\sin(\theta) = \dfrac{1}{x}$. Drawing a triangle for this yields the following picture:
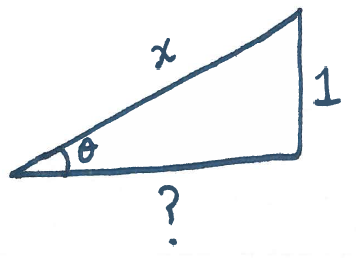
To find the missing side labelled $?$, use the Pythagorean Theorem to write
$$?^2 + 1^2 = x^2,$$
and solve for $?$ to get
$$? = \sqrt{x^2-1}.$$
Therefore compute
$$\cos\left(\sin^{-1}\left(\dfrac{1}{x} \right)\right) = \cos(\theta)= \dfrac{\sqrt{x^2-1}}{x}.$$
Note: Wolfram alpha gives $\sqrt{1 - \dfrac{1}{x^2}}$, which is equivalent because
$$\dfrac{\sqrt{x^2-1}}{x} = \sqrt{\dfrac{x^2-1}{x^2}} = \sqrt{1-\dfrac{1}{x^2}}.$$
