Back to the class
Section 4.1 #29: Given the following probability distribution:
| Dogs | 0 | 1 | 2 | 3 | 4 | 5 |
| Probability | 0.686 | 0.195 | 0.077 | 0.022 | 0.013 | 0.0007 |
Find the mean, variance, and standard deviation, and
Solution: First compute the mean:
$$\mathrm{mean} = \displaystyle\sum x P(x)= 0(0.686)+1(0.195)+2(0.077)+3(0.022)+4(0.013)+5(0.0007)=0.4705.$$
The variance is
$$\begin{array}{ll}
\sigma^2 &= \displaystyle\sum (x-\mu)^2P(x) \\
&=(0- 0.4705)^2(0.686)+(1-0.4705)^2(0.195)+(2-0.4705)^2(0.077)+(3-0.4705)^2(0.022)+(4-0.4705)^2(0.013)+(5-0.4705)^2(0.0007) \\
&=0.7037
\end{array}$$
The standard deviation is
$$\sigma=\sqrt{\sigma^2}=\sqrt{0.7037}=0.8388.$$
Section 4.2 #16: Thirty-nine percent of U.S. adults think that the government should help fight childhood obesity. You randomly select six U.S. adults. Find the probability that the number of U.S. adults who think that the governmnet hsould help fight childhood obesity is
a.) exactly two,
b.) at least four, and
c.) less than three.
Solution: This is a binomial experiment with $n=6$, $p=0.39$, and $q=1-p=0.61$. The probability distribution function is given by the following, for $x=0,1,2,3,4,5,6$:
$$P(x)=\dfrac{6!}{(6-x)!x!} (0.39)^x (0.61)^{6-x}.$$
For part a.), compute
$$P(2)=\dfrac{6!}{(6-2)!2!}(0.39)^2 (0.61)^{6-2}=\dfrac{6!}{4!2!} (0.39)^2 (0.61)^4 = 0.3158$$
For part b.), compute
$$P(4)+P(5)+P(6)=\dfrac{6!}{2!4!}(0.39)^4(0.61)^2+\dfrac{6!}{5!1!}(0.39)^5(0.61)^1 + \dfrac{6!}{6!0!} (0.39)^6(0.61)^0 =0.1656$$
For part c.), compute
$$P(0)+P(1)+P(2)=\dfrac{6!}{0!6!}(0.39)^0(0.61)^6 + \dfrac{6!}{1!5!}(0.39)^1(0.61)^5+\dfrac{6!}{2!4!}(0.39)^2(0.61)^4=0.5650$$
Section 4.3 #11: The probability that you will make a sale on any given telephone call is $0.19$. Find the probability that you
a.) make your first sale on the fifth call,
b.) make your first sale on the first, second, or third call, and
c.) do not make a sale on the first three calls.
Solution: First note that the random variable here is geometric with $p=0.19$ and $q=1-p=0.81$. It has probability distribution
$$P(x)=pq^{x-1}=(0.19)(0.81)^{x-1}.$$
For part a.), compute
$$P(5)=(0.19)(0.81)^{5-1}=0.08178.$$
For part b.), compute
$$P(1)+P(2)+P(3)=(0.19)(0.81)^{1-1} + (0.19)(0.81)^{2-1} + (0.19)(0.81)^{3-1}=0.4685.$$
For part c.), compute using "complements" and the result from part b.):
$$\begin{array}{ll}
P(x > 3) &= 1-P(x \leq 3) \\
&= 1- (P(0)+P(1)+P(2)+P(3))
&= 1- 0.4685 \\
&= 0.5315.
\end{array}$$
Section 4.3 #13: The mean number of births per minute in the United States in a recent year as about eight. Find the probability that the number of births in any given minute is
a.) exactly five,
b.) at least five, and
c.) more than five.
Solution: First note that the random variable here is Poisson with $\mu=8$. It has probability distribution
$$P(x)=\dfrac{8^x e^{-8}}{x!},$$
where $e$ is the special number $e=2.718281\ldots$. For part a.), compute
$$P(5)=\dfrac{8^5 e^{-8}}{5!}=0.09160.$$
For part b.), compute
$$\begin{array}{ll}
P(x \geq 5) &= 1-P(x < 5) \\
&= 1- (P(0)+P(1)+P(2)+P(3)+P(4)) \\
&= 1- \left( \dfrac{8^0e^{-8}}{0!} + \dfrac{8^1e^{-8}}{1!} + \dfrac{8^2 e^{-8}}{2!} + \dfrac{8^3e^{-8}}{3!} + \dfrac{8^4 e^{-8}}{4} \right) \\
&=0.9003
\end{array}$$
For part c.), compute using the results in part a.) and part b.):
$$P(x>5)=1-P(x \leq 5)=1-(P(x=5)+P(x<5))=1-(0.09160+0.9003)=0.8087.$$
Section 5.1 #15: Determine whether the graph could represent a variable with a normal distribution:
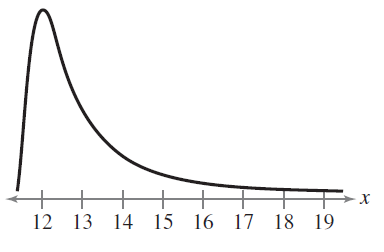
Solution: It could not represent a normal distribution -- it is not a symmetric graph.
Section 5.1 #21: Find the area of the indicated region in the standard normal curve:
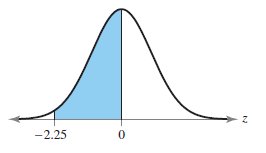
Solution: We understand this probability as the probability $P(-2.25 < z < 0)$. To calculate it using the standard normal table, we compute
$$P(-2.25 < z < 0) = P(z < 0) - P(z < -2.25) = 0.5 - 0.0122=0.4878.$$
Section 5.1 #27: Find the area under the standard normal curve to the right of $z=-0.65$.
Solution: We are being asked to compute $P(z > -0.65)$. Since the standard normal table only allows us to read values of the form $P(z < \#)$, we must rewrite the probability and look it up as follows:
$$P(z > -0.65) = 1- P(z \leq -0.65) = 1-0.2578=0.7422.$$




