Back to the class
Quiz 8
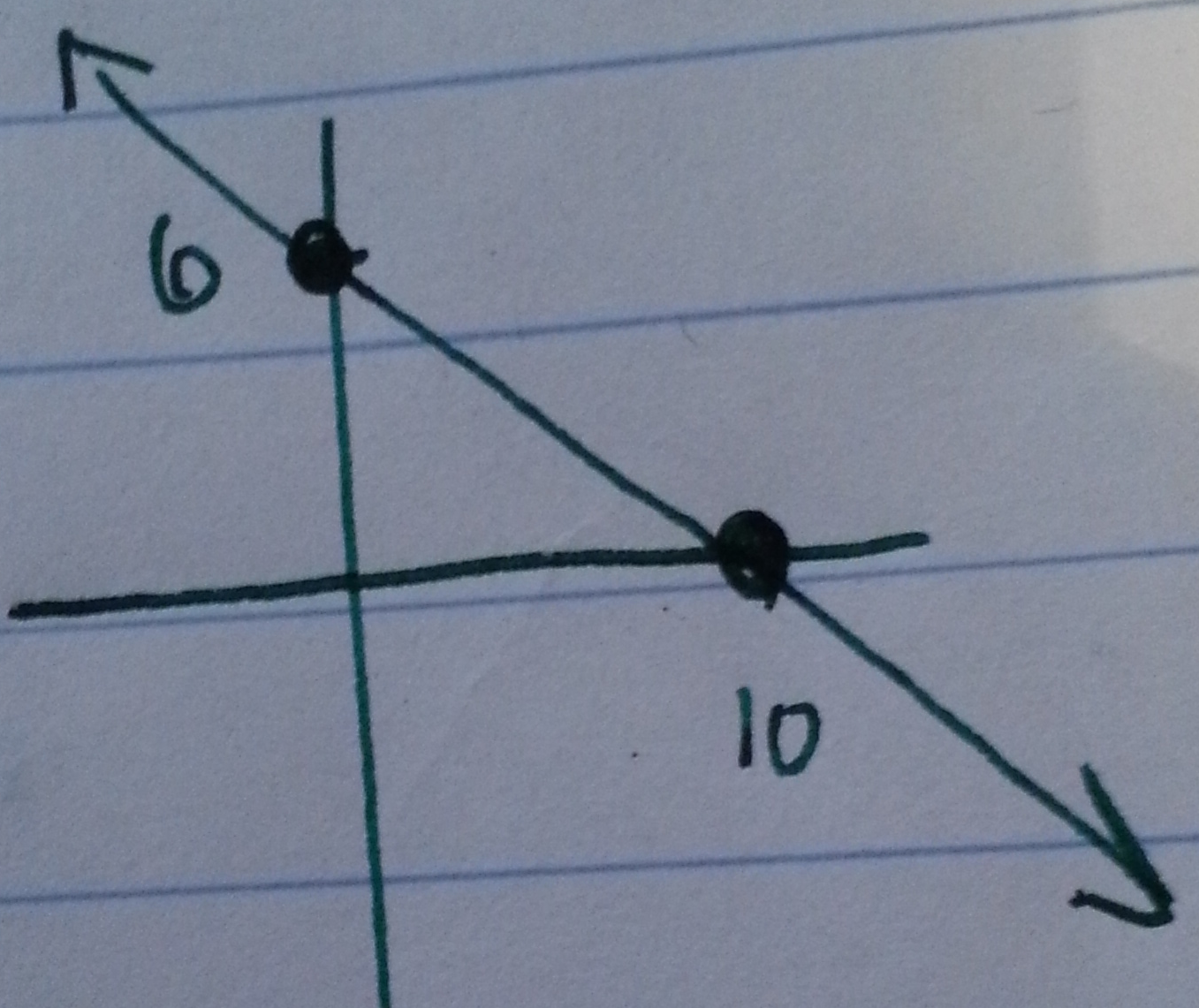
1. Use intercepts to graph $3x+5y=30$.
Solution: To find the $x$-intercept, set $y=0$ to get the equation $3x=30$ yielding the value $x=\dfrac{30}{3}=10$. Therefore the $x$-intercept is $(10,0)$. To find the $y$-intercept set $x=0$ to get the equation $5y=30$ yielding the value $y=\dfrac{30}{5}=6$. Therefore the $y$-intercept is $(0,6)$. Plot these points and connect the dots to complete the problem:
2. Solve by graphing: $\left\{ \begin{array}{ll}
y=x+1 \\
y=-x-1 \\
\end{array} \right.$
Solution: The $y$-intercept of the first equation is $(0,1)$ and the $x$-intercept of the first equation is $(-1,0)$. The $y$-intercept of the second equation is $(0,-1)$ and the $x$-intercept is $(-1,0)$. Plot these and observe the intersection point to solve the system:
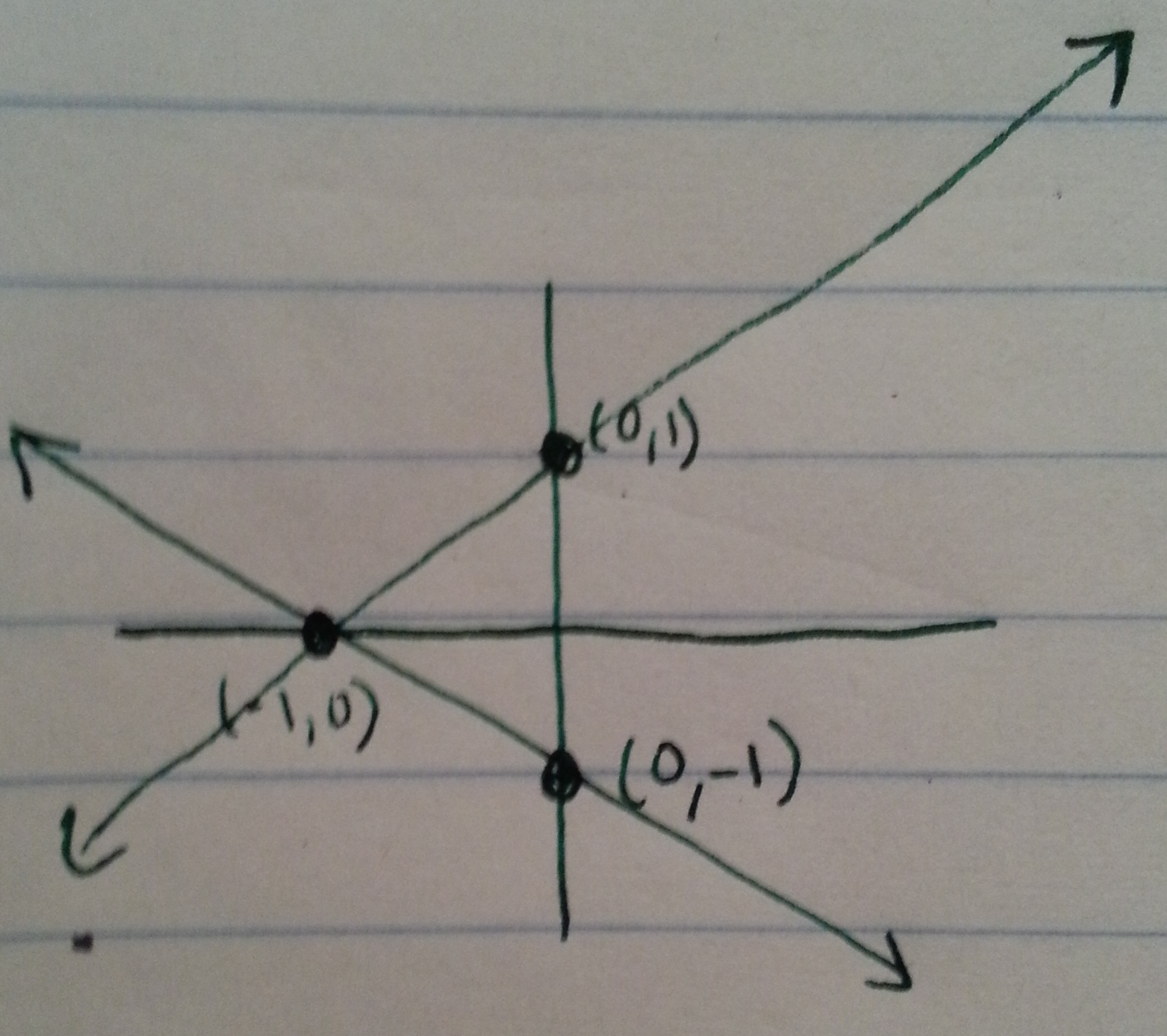
the intersection point is at $(-1,0)$, which is the solution.
3. Solve algebraically: $\left\{ \begin{array}{ll}
y=x+1 & (i) \\
y=-x-1 & (ii) \\
\end{array} \right.$
Solution: Plug $y$ from equation (i) into equation (ii):
$$x+1=-x-1,$$
add $x$ to both sides to get
$$2x+1=-1,$$
add $-1$ to both sides to get
$$2x=-2,$$
now divide by $2$ to get $x=-1$. Take this value of $x$ and plug it into one of the two equations in the system, say (i), to get $y=(-1)+1=0$. Therefore the solution is $(-1,0)$.
4. Solve algebraically: $\left\{ \begin{array}{ll}
3x+6y=9 & (i) \\
3x-y=9 & (ii).
\end{array} \right.$
Solution: From equation (ii), solve for $y$ to get
$$y=3x-9.$$
Plug this value of $y$ into (i) to get
$$3x+6(3x-9)=9.$$
Expand the left hand side to get
$$3x+18x-54=9.$$
Simplify the left and add $54$ to get
$$21x=63.$$
Divide by $21$ to get
$$x= \dfrac{63}{21} = 3.$$
Plug this value of $x$ into, say (i), to see that
$$3(3)+6y=9.$$
Simplify the left to get
$$9+6y=9.$$
Subtract $9$ to get
$$6y=0,$$
and finally divide by $6$ to get
$$y=0.$$
We have found the solution $(3,0)$.
5. Find an angle coterminal with $32^{\circ}$.
Solution: All angles coterminal with a given angle are found by adding or subtracting a multiple of $360^{\circ}$. So we could use,
$$32^{\circ} + 360^{\circ} = 392^{\circ},$$
or many other possibilities.




