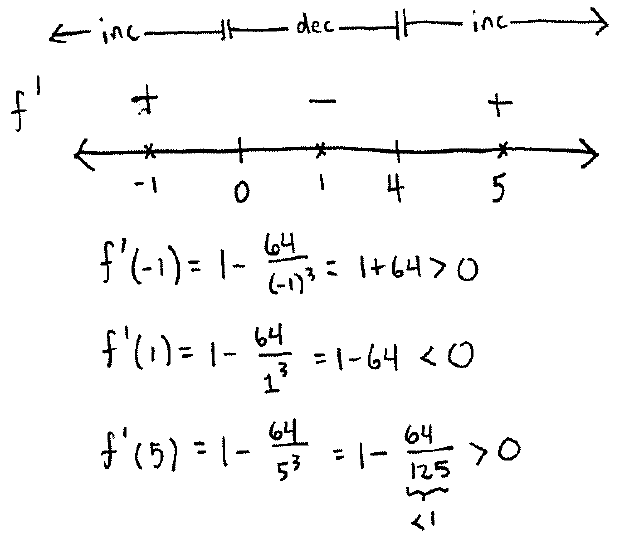Back to the class
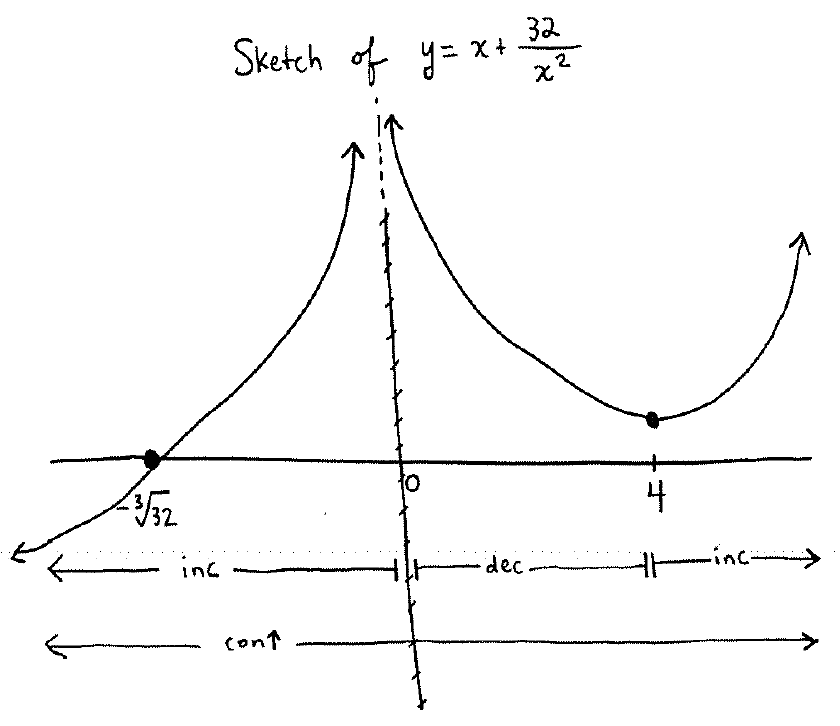
Section 3.6 #11: Sketch the graph of $f(x)=x+\dfrac{32}{x^2}$.
Solution: First we take two derivatives of $f$: the first derivative
$$f'(x)=1-\dfrac{64}{x^3},$$
and the second derivative
$$f''(x)=\dfrac{192}{x^4}.$$
Find the critical points: firstly, $f'$ is undefined at $x=0$ and secondly, consider the equation $f'(x) \stackrel{\rm{set}}{=} 0$:
$$1- \dfrac{64}{x^3}=0.$$
This yields the equation
$$1 = \dfrac{64}{x^3}.$$
Multiply by $x^3$ (keeping in mind we are now taking $x \neq 0$) to get
$$x^3 = 64.$$
Therefore
$$x = \sqrt[3]{64}=4.$$
(note there is no $\pm$ here... that only appears when taking an even root!)
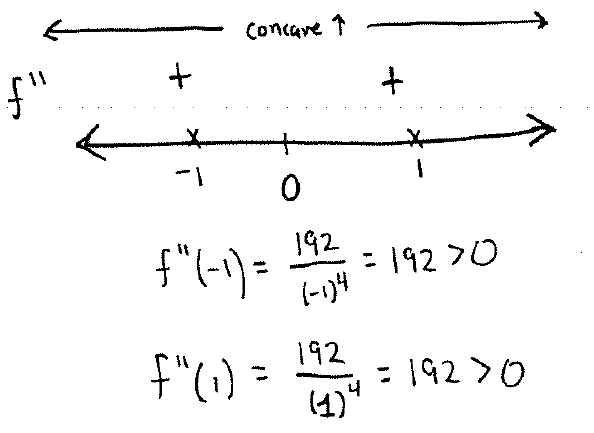
We have found the following critical points: $x=0$ and $x=4$. We should also find possible inflection points by asking where $f''$ is undefined, which is at $x=0$, and also consider solutions of the equation $f''(x) \stackrel{\rm{set}}{=} 0$:
$$\dfrac{192}{x^4} = 0.$$
Multiplying by $x^4$ (which we are thinking of nonzero here) yields the equation $192=0$ which has no solutions. So the only possible inflection point is at $x=0$.
Now find the intervals of increasing and decreasing:
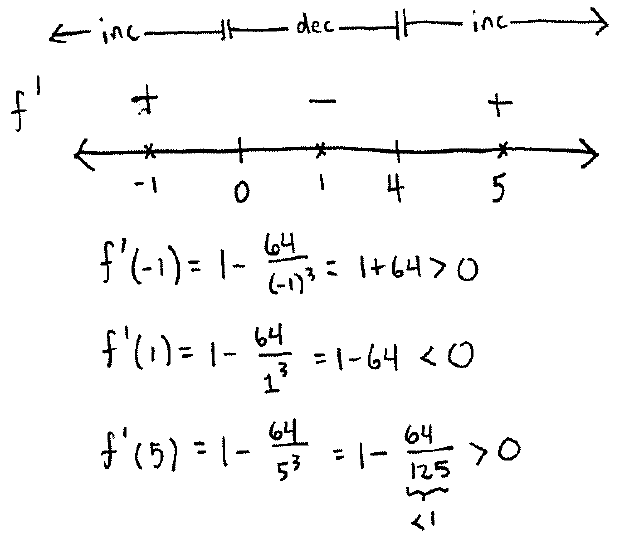
Now find the concavity behavior:
Finally find any $x$-intercepts by solving $f(x) \stackrel{\rm{set}}{=} 0$:
$$x + \dfrac{32}{x^2} = 0.$$
Multiply by $x^2$ to get $x^3 + 32 = 0.$ To solve, subtract by $32$ and take the cube root to get
$$x = \sqrt[3]{-32}=-\sqrt[3]{32}.$$
This means the point $(-\sqrt[3]{32},0)$ is on the graph of $f$. Also check to see if a $y$-intercept exists by trying to evaluate $f(0)$ --- it turns out that $f$ is not defined at zero and has an asymptote there.
Take all of this information together to sketch the graph:
Section 3.7 #8: Find two positive numbers that that satisfies the following property: the sum of the first number squared and the second number is $54$ and the product is a maximum.
Solution: Call these numbers $x$ and $y$. We need to optimize the value
$$P=xy$$
subject to the constraint that
$$x^2+y=54.$$
It is most natural to solve the constraint for $y$ and plug it into the formula for $P$:
$$y=54-x^2$$
yielding
$$P=x(54-x^2)=54x-x^3.$$
We must now maximize $P$. We will do so with the second derivative test (the first derivative test would also work). Compute
$$P'=54-3x^2$$
and
$$P''=-6x.$$
First find the critical points by solving $P' \stackrel{\rm{set}}=0$:
$$54 = 3x^2,$$
so since $\dfrac{54}{3}=18$, we get
$$18 = x^2.$$
Solving for $x$ yields the two critical points
$$x = \pm \sqrt{18} = \pm 3 \sqrt{2}.$$
We are told that $x$ and $y$ must be positive numbers in the wording of the problem, so we throw out the negative solution, leaving us the only critical point $x=3\sqrt{2}$.
Now to use the second derivative test, plug these critical points into $P''$ to get
$$P''(3\sqrt{2})=-6(3\sqrt{2})=-18\sqrt{2} < 0,$$
showing that $P$ has a maximium at $x=3\sqrt{2}$. The problem asked for both numbers, so now we may find the value of $y$ by plugging into the equation $y=54-x^2$:
$$y=54-(3\sqrt{2})^2=54-18=36.$$
Section 3.7 #35: The sum of the perimeters of an equilateral triangle and a square is $10$. Find the dimensions of the triangle and the square that produce a minimum total area.
Solution: First draw the triangle and the square. Label the sides appropriately:
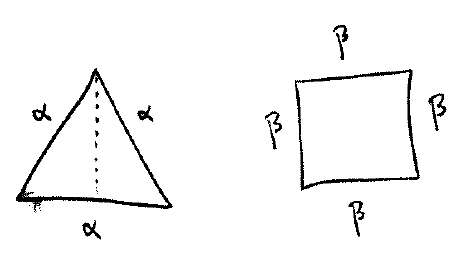
Now recall that the area of this square is $\beta^2$ and the area of any triangle is $\dfrac{1}{2} \rm{base} \times \rm{height}$. We must find the height of the given triangle (the base is $\alpha$). To do this, bisect the triangle to get the following:
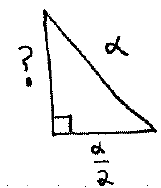
To find the height (we labeled it as "$?$"), use the Pythagorean theorem to get
$$\left( \dfrac{\alpha}{2} \right)^2 + ?^2 = \alpha^2,$$
which yields
$$?^2 = \alpha^2 - \dfrac{\alpha^2}{4} = \dfrac{3}{4} \alpha^2.$$
Taking the square root yields
$$? = \pm \sqrt{ \dfrac{3}{4} \alpha^2} = \pm \dfrac{\sqrt{3}}{2} \alpha.$$
Since $?$ represents the length of a triangle, we take the positive value. This means the equilateral triangle has base $\alpha$ and height $\dfrac{\sqrt{3}}{2}\alpha$. Hence the area of the equilateral triangle is
$$\dfrac{1}{2} \cdot \alpha \cdot \dfrac{\sqrt{3}}{2} \alpha = \dfrac{\sqrt{3}}{4}\alpha^2.$$
Therefore the quantity we must optimize is
$$A = \mathrm{area}_{\mathrm{square}}+\mathrm{area}_{\mathrm{triangle}}=\beta^2 + \dfrac{\sqrt{3}}{4} \alpha^2.$$
What is the constraint? We were told the sum of the perimeters of the figures is $10$. The perimeter of the square is $4\beta$ and the perimeter of the triangle is $3\alpha$, therefore the constraint is
$$4\beta + 3\alpha = 10.$$
Solving the constraint for, say, $\beta$, yields
$$\beta=\dfrac{10-3\alpha}{4}.$$
Consequently
$$\beta^2=\dfrac{100-60\alpha+9\alpha^2}{16}.$$
Plug this into our equation for the area to get
$$A=\dfrac{100-60\alpha+9\alpha^2}{16} + \dfrac{4\sqrt{3}}{16} \alpha^2 = \dfrac{(9+4\sqrt{3})\alpha^2-60\alpha+100}{16}.$$
To find the critical point, differentiate and set the derivative equal to zero to get
$$A'=\dfrac{(18+8\sqrt{3})\alpha-60}{16} \stackrel{\rm{set}}{=} 0.$$
Solve this by multiplying by $16$ to get
$$(18+8\sqrt{3})\alpha - 60 = 0.$$
Add $60$ and divide by $18+8\sqrt{3}$ to get
$$\alpha = \dfrac{60}{18+8\sqrt{3}} = \dfrac{30}{9+4\sqrt{3}}.$$
To show this is a minimum, we will use the second derivative test. Compute
$$A''=\dfrac{18+8\sqrt{3}}{16},$$
a constant function. Therefore if we plug the critical point in to $A''$ we get
$$A'' \left( \dfrac{30}{9+4\sqrt{3}} \right) = \dfrac{18+8\sqrt{3}}{16} > 0.$$
So the critical point is a minimum ("horizontal tangent and concave up --> minimum"), as desired. Finally, the value of $\beta$ may be found by plugging into our constraint equation:
$$\beta = \dfrac{10-3\left(\frac{30}{9+4\sqrt{3}} \right)}{4} = \dfrac{10\sqrt{3}}{9+4\sqrt{3}}.$$
Problem B:Find all functions $f$ with the property that $f'(x)=3x^2+2x+4$, that is, find $D^{-1}(3x^2+2x+4)$.
Solution: Using the rules of anti-differentiation we get
$$\begin{array}{ll}
D^{-1}(3x^2+2x+4) &= 3 D^{-1}(x^2) + 2 D^{-1}(x) + 4 D^{-1}(1) \\
&= 3 \left( \dfrac{x^3}{3} \right) + 2 \left( \dfrac{x^2}{2} \right) + 4x + C \\
&= x^3 + x^2 + 4x + C.
\end{array}$$
Problem C: Compute the sum $\displaystyle\sum_{k=0}^5 k^2+1$.
Solution: The sum is
$$\begin{array}{ll}
\displaystyle\sum_{k=0}^5 k^2+1 &= (0^2+1) + (1^2+1) + (2^2+1) + (3^2+1) + (4^2+1) + (5^2+1) \\
&= 1 + 2 + 5 + 10 + 17 + 26 \\
&= 61.
\end{array}$$