.
KE8QZC | DCAA | AMC | SFW | TSW
ORCID iD icon

Back to the class
Section 4.1 #29: Solve the right triangle which is given by the information $b=5$ and $B=20^{\circ}$.
Solution: First draw the described triangle:

Solve for $A$
We use the sum of the angles of triangle being $180^{\circ}$ to write $$90^{\circ} + 20^{\circ} + A = 180^{\circ}.$$ Solving for $A$ yields $$A = 180^{\circ} - 20^{\circ} - 90^{\circ} = 70^{\circ}.$$ Solve for $c$
$$\sin\left( 20^{\circ} \right) = \dfrac{5}{c}.$$ Therefore $$c = \dfrac{5}{\sin\left(20^{\circ}\right)}.$$ Solve for $a$
One could use the Pythagorean theorem for this, but it is easier to simply notice that $$\tan\left(20^{\circ} \right) = \dfrac{5}{a},$$ so $$a = \dfrac{5}{\tan\left(20^{\circ}\right)}.$$

Section 4.2 #31: Solve the triangle given by the information $b=4$, $c=6$, and $B=20^{\circ}$.
Solution: First draw the described triangle:

Solve for $C$
Using the law of sines, $$\dfrac{\sin\left(20^{\circ}\right)}{4} = \dfrac{\sin(C)}{6}.$$ Therefore $$\sin(C) = \dfrac{6\sin\left( 20^{\circ} \right)}{4}.$$ To isolate $C$ take $\sin^{-1}$ of both sides (recall that $\sin^{-1}(\sin(C))=C$) to get $$C = \sin^{-1} \left( \dfrac{6\sin \left( 20^{\circ} \right)}{4} \right) = 30.87^{\circ}.$$ We must also check the other possible value of $C$: $$C = 180^{\circ}-30.87^{\circ} = 149.13^{\circ}.$$ This angle is not too big and so we will have to consider two possible triangles -- one with $C=30.87^{\circ}$ and the other with $C=149.13^{\circ}$.
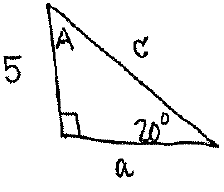
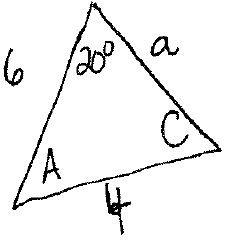
Solve for $A$ in the $C=30.87$ triangle
Use the fact that the sum of angles in a triangle is $180^{\circ}$ to see $$20^{\circ} + 30.87^{\circ} + A = 180^{\circ}.$$ Therefore $$A = 180^{\circ} - 20^{\circ} - 30.87^{\circ} = 129.13^{\circ}.$$ Solve for $a$ in the $C=30.87$ triangle
By the law of sines, $$\dfrac{\sin\left(129.13^{\circ} \right)}{a}= \dfrac{\sin \left( 20^{\circ} \right)}{4},$$ so $$a = \dfrac{4\sin \left( 129.13^{\circ} \right)}{\sin \left(20^{\circ} \right)}.$$
Solve for $A$ in the $C=149.13$ triangle
Use the fact that the sum of angles in a triangle is $180^{\circ}$ to see $$20^{\circ} + 149.13^{\circ} + A = 180^{\circ}.$$ Therefore $$A = 180^{\circ} - 20^{\circ} - 149.13^{\circ}=10.87^{\circ}.$$ Solve for $a$ in the $C=149.13$ triangle
By the law of sines, $$\dfrac{\sin \left( 10.87^{\circ} \right)}{a} = \dfrac{\sin(20^{\circ})}{4},$$ so $$a = \dfrac{4 \sin \left( 10.87^{\circ} \right)}{\sin(20^{\circ})}.$$























Section 4.2 #32: Solve the triangle given by the information $a=3$, $b=7$, and $A=70^{\circ}$.
Solution: First draw the triangle:

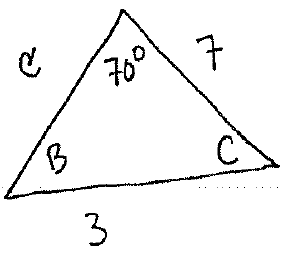Find $B$
By the law of sines we see $$\dfrac{\sin(B)}{7} = \dfrac{\sin(70^{\circ})}{3}.$$ Therefore $$\sin(B) = \dfrac{7\sin(70^{\circ})}{3} = 2.19.$$ But we may not take $\sin^{-1}$ of $2.19$ (it is too big) and so this triangle does not exist.

Section 4.3 #15: Solve the triangle given by the information $a=9$, $b=6$, and $c=4$.
Solution: First draw the triangle:

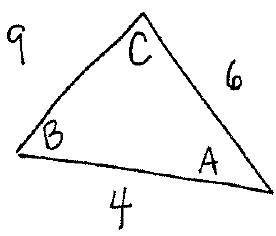
We have no choice other than to use the law of cosines to solve for the angles.
Solve for $A$
Using the law of cosines, we see $$9^2 = 6^2 + 4^2 - 2(6)(4)\cos(A).$$ This means $$81 = 36 + 16 - 48\cos(A).$$ Isolating $\cos(A)$ gives us $$\cos(A) = \dfrac{-29}{48}.$$ Therefore take $\cos^{-1}$ to isolate $A$: $$A = \cos^{-1} \left( -\dfrac{29}{48} \right) = 127.2^{\circ}.$$ Solve for $B$
Using the law of cosines, we see $$6^2 = 9^2 + 4^2 - 2(9)(4)\cos(B).$$ Simplifying yields $$36 = 81 + 16 - 72\cos(B).$$ Isolating $\cos(B)$ yields $$\cos(B) = \dfrac{-61}{-72}.$$ Therefore take $\cos^{-1}$ to get $$B = \cos^{-1} \left( \dfrac{-61}{-72} \right) =32.09^{\circ}.$$ Solve for $C$
We will use the fact that the sum of the angles in a triangle is $180^{\circ}$. This yields $$127.2^{\circ} + 32.09^{\circ} + C = 180^{\circ},$$ so $$C = 180^{\circ}-127.2^{\circ} - 32.09^{\circ} = 20.71^{\circ}.$$ NOTE: you can solve this any way you wish, you may get slightly different answers depending on what angles you solve for first/etc -- you may also just use the law of cosines three times instead of using the sum of angles formula

Section 4.3 #20: Solve the triangle given by the information $a=6$, $b=4$, and $C=60^{\circ}$.
Solution: First draw the triangle:

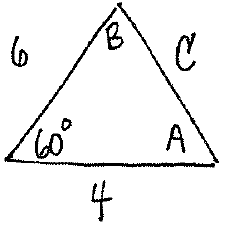
Solve for $c$
Using the law of cosines, $$c^2 = 6^2+4^2-2(6)(4)\cos \left( 60^{\circ} \right),$$ so $$c= \sqrt{52-48\cos \left( 60^{\circ} \right)} = 5.29.$$ There are two missing angles. We will use the law of cosines to find one of the missing angles and then use the sum of the angles equalling $180^{\circ}$ to find the third.
Find $B$
Using the law of cosines, $$4^2 = 6^2 + 5.29^2 - 2(6)(5.29)\cos \left( B \right),$$ yielding $$\dfrac{-47.98}{-63.48} = \cos(B),$$ so take $\cos^{-1}$ of each side to get $$B = \cos^{-1} \left( \dfrac{-47.98}{-63.48} \right)=40.9^{\circ}.$$ Find $A$ $$A = 180^{\circ} - 60^{\circ} - 40.9^{\circ} = 79.1^{\circ}.$$