Back to the class
1.) Let $f(x)=x^2+1$ and $g(x)=\sqrt{x-7}$. What is...
a.) $(f \circ g)(x)$?
b.) $(g \circ f)(x)$?
c.) $(f \circ f)(x)$?
d.) $(g \circ g)(x)$?
Solution:
a.) Compute
$$\begin{array}{ll}
(f \circ g)(x) &= f(g(x)) \\
&= f(\sqrt{x-7}) \\
&= (\sqrt{x-7})^2+1 \\
&= x-7+1 \\
&= x-6.
\end{array}$$
b.) Compute
$$\begin{array}{ll}
(g \circ f)(x) &= g(f(x)) \\
&= g(x^2+1) \\
&= \sqrt{(x^2+1)-7} \\
&= \sqrt{x^2-6}.
\end{array}$$
c.) Compute
$$\begin{array}{ll}
(f \circ f)(x) &= f(x^2+1) \\
&= (x^2+1)^2 + 1 \\
&= (x^4 + 2x^2 + 1) + 1 \\
&= x^4 + 2x^2 + 2.
\end{array}$$
d.) Compute
$$\begin{array}{ll}
(g \circ g)(x) &= g(g(x)) \\
&= g(\sqrt{x-7}) \\
&= \sqrt{\sqrt{x-7}-7}.
\end{array}$$
2.) Decompose the function $h(x)=\dfrac{1}{\sqrt{x^2-5}}$ by finding functions $f(x)$ and $g(x)$ such that
$$h(x) = (f \circ g)(x).$$
Solution: There are many ways to do this. One way is to let $f(x)=\dfrac{1}{x}$ and $g(x)=\sqrt{x-7}$ which yields
$$(f \circ g)(x) = f(g(x)) = f(\sqrt{x-7})=\dfrac{1}{\sqrt{x-7}}.$$
Another way would be to let $f(x)=\dfrac{1}{\sqrt{x}}$ and let $g(x)=x-7$ so that
$$(f \circ g)(x) = f(g(x)) = f(x-7) = \dfrac{1}{\sqrt{x-7}}.$$
3.) Do the following graphs exhibit any symmetry? If so, what kind(s)?
a.) 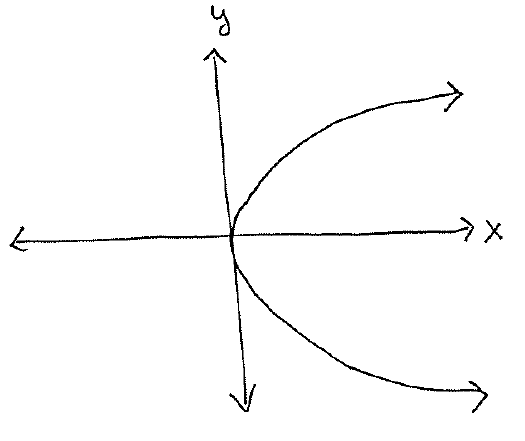
b.) 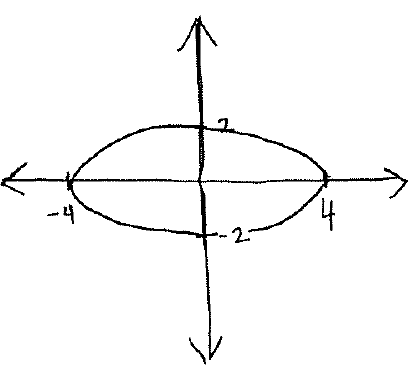
c.) 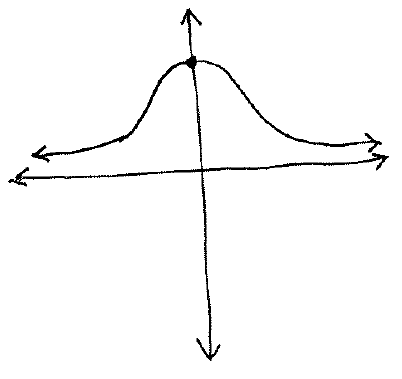
Solution:
a.) Symmetric with respect to the $x$-axis.
b.) Symmetric with respect to the $x$-axis, with respect to the $y$-axis, and with respect to the origin.
c.) Symmetric with respect to the $y$-axis.





