Back to the class
1.) Let
$$f(x) = \left\{ \begin{array}{ll}
x+2, & x \geq 3 \\
-x+9, & x < 3.
\end{array} \right.$$
Graph $f(x)$.
Solution: Since the graph of $y=x+2$ is
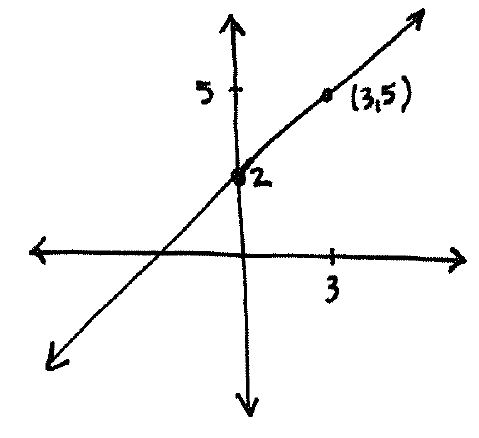
and the graph of $y=-x+9$ is
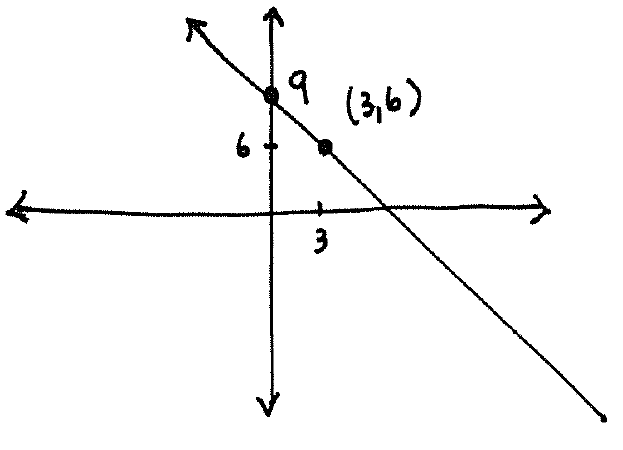 ,
,
we see that the graph of $y=f(x)$ is
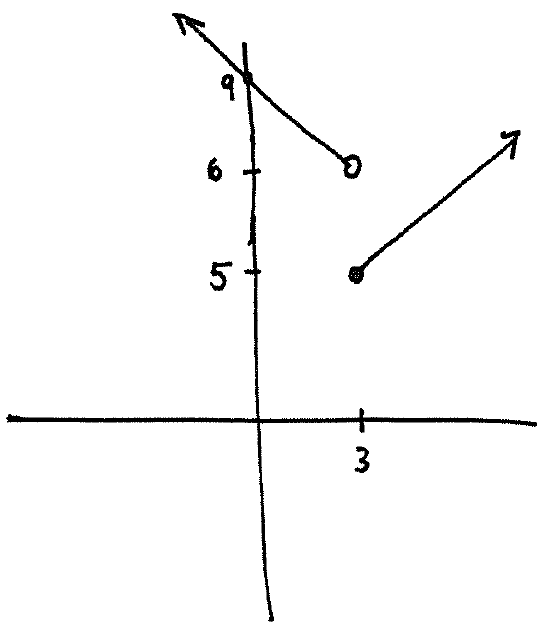 .
.
2.) Consider the following graph:
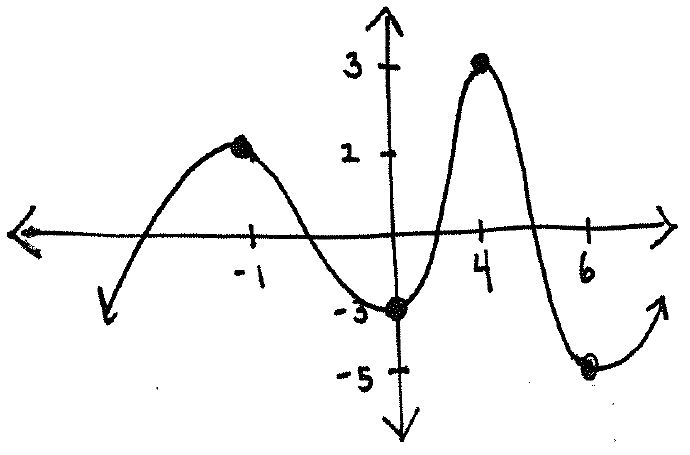
a.) Where is the following function increasing and decreasing?
b.) Where are its relative maximums and minimums (if any)?
c.) What are the value(s) of any relative maximums or minimums found in part (b)?
Solution:
a.) The function is increasing on $(-\infty,-1) \cup (0,4) \cup (6,\infty)$. The function is decreasing on $(-1,0) \cup (4,6)$.
b.) The relative maximums occur at the $x$-values $-1$ and $4$. The relative minimums occur at the $x$-values $0$ and $6$.
c.) The value of the relative max at $x$-value $-1$ is the $y$-value $1$. The value of the relative max at the $x$-value $4$ is the $y$-value $3$. The value of the relative minimum at $x$-value $0$ is the $y$-value $-3$. The value of the relative minimum at $x$-value $6$ is the $y$-value $-5$.
3.) Given the following graph:
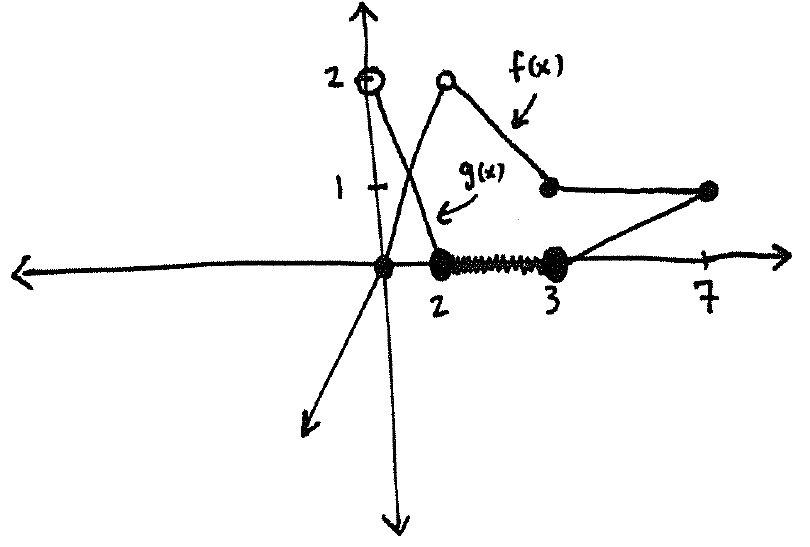
a.) What is the domain of $f$?
b.) What is the domain of $\dfrac{g}{f}$?
c.) What is the domain of $\dfrac{f}{g}$?
d.) What is the value of $(f+g)(3)$?
Solution:
a.) The domain of $f$ is $[0,2) \cup (2,7]$.
b.) The domain of $\dfrac{g}{f}$ is the domain of $g$ intersected with the domain $f$ and removing the $x$-values where $f$ is zero, i.e. $(0,2) \cup (2,7]$.
c.) The domain of $\dfrac{f}{g}$ is the domain of $f$ intersected with the domain of $g$ and removing the $x$-value where $g$ is zero, i.e. $(0,2) \cup (3,7]$.
d.) Compute directly: $(f+g)(3)=f(3)+g(3)=1+0=1$.




 ,
, .
. 
