AMPS | THARC | KE8QZC | SFW | TSW
ORCID iD icon

Back to undergraduate research page
Zeta functions on time scales?
Let $\mathbb{T}=\{\ldots,t_{-1},t_0,t_1,\ldots\}$ be a time scale of isolated points such that $0 \not\in \mathbb{T}$. Define a zeta function on time scales for complex $z$ by $$\zeta_{\mathbb{T}}(z) = \displaystyle\int_{\mathbb{T}} \dfrac{1}{\tau^z} \Delta \tau=\displaystyle\sum_{k=-\infty}^{\infty} \dfrac{\mu(t_k)}{t_k^z},$$ where $\mu$ denotes the forward graininess function $\mu(t_k)=t_{k+1}-t_k$.

The factor of $\mu$ in the numerator could be a problem. So another possible definition for this could be $$\tilde{\zeta}_{\mathbb{T}}(z) = \displaystyle\int_{\mathbb{T}} \dfrac{1}{\mu(\tau) \tau^z} \Delta \tau= \displaystyle\sum_{k=-\infty}^{\infty} \dfrac{1}{t_k^z},$$ What can we say about this?
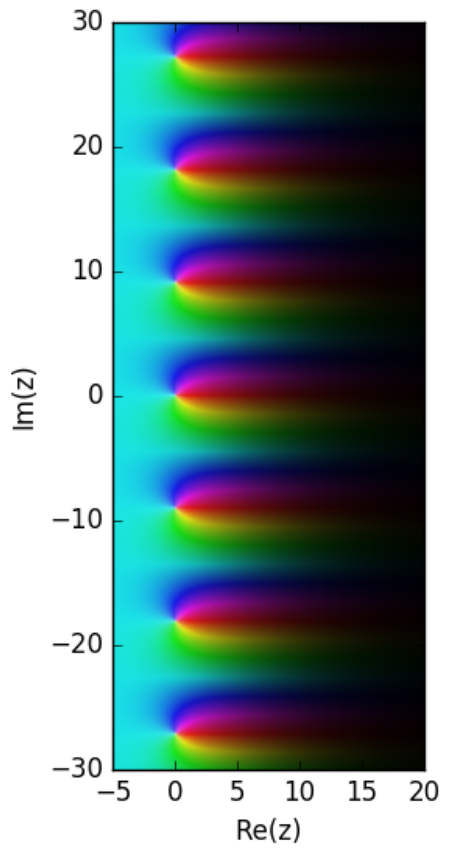
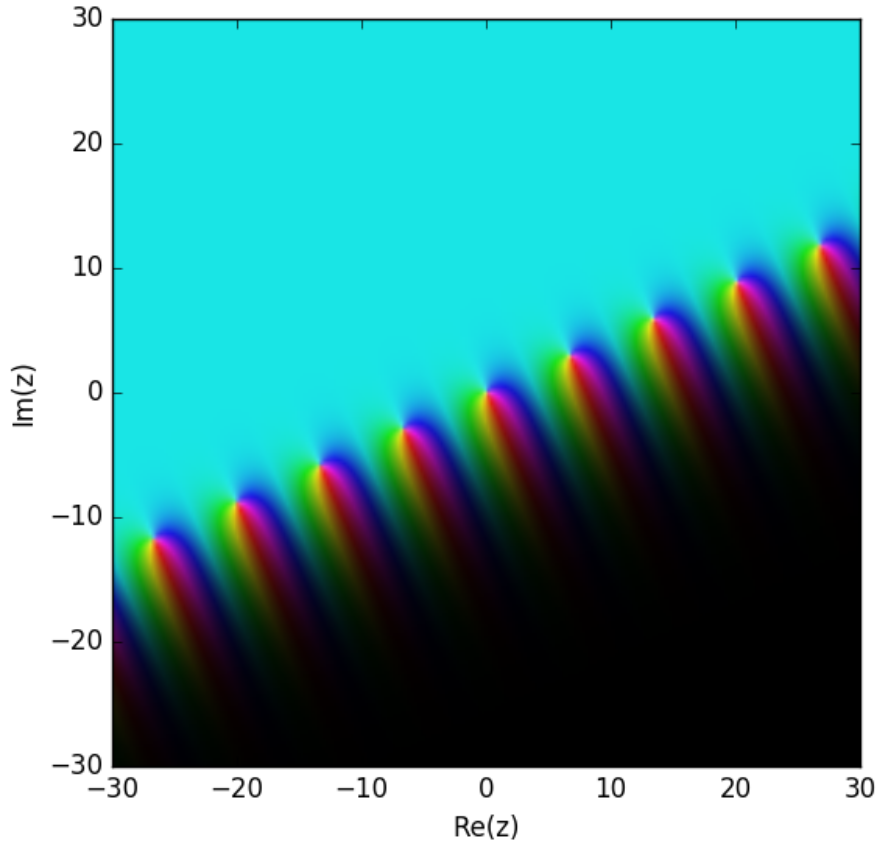
Time scale (of isolated points) $\mu(t)$ $\zeta_{\mathbb{T}}(z)=\displaystyle\sum_{k=-\infty}^{\infty} \dfrac{\mu(t_k)}{t_k^z}$$\tilde{\zeta}_{\mathbb{T}}(z)=\displaystyle\sum_{k=-\infty}^{\infty} \dfrac{1}{t_k^z}$
$\mathbb{Z}^+=\{1,2,3,\ldots\}$1$\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{k^z}=\zeta(z), \mathrm{Re}(z)>1$ (Riemann zeta function)same because $\mu \equiv 1$
$2^{\mathbb{N}_0}=\{1,2,4,8,\ldots\}$t$\displaystyle\sum_{k=1}^{\infty} \dfrac{2^k}{2^{kz}}=\dfrac{2}{2^z-2}$;$2^{\mathrm{Re}(z)}>2$$\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{2^{kz}}=\dfrac{2^z}{2^z-1}; 2^{\mathrm{Re}(z)}>1$
$3^{\mathbb{N}_0}=\{1,3,9,27,\ldots\}$2t$2\displaystyle\sum_{k=0}^{\infty} \dfrac{3^k}{3^{kz}} =2\dfrac{3^z}{3^z-3}; 2^{\mathrm{Re}(z)}>2$$\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{3^{kz}} = \dfrac{3^z}{3^z-1}; 3^{\mathrm{Re}(z)}>1$
$q^{\mathbb{N}_0}=\{1,q,q^2,\ldots\},q>1$ (quantum)$(q-1)t$$(q-1)\displaystyle\sum_{k=0}^{\infty} \dfrac{q^k}{q^{kz}}=(q-1)\dfrac{q^z}{q^z-q}; q^{\mathrm{Re}(z)}>q$$\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{q^{kz}}=\dfrac{q^z}{q^z-1}; q^{\mathrm{Re}(z)}>1$
$\{1,4,9,16,25,\ldots\}$ (nonzero square integers)$2\sqrt{t}+1$$\displaystyle\sum_{k=1}^{\infty} \dfrac{2k+1}{k^{2z}}; \mathrm{Re}(z)>1$$\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{k^{2z}}=\zeta(2z); 2\mathrm{Re}(z)>1$ (Riemann zeta function)
$h\mathbb{Z}^+=\{h,2h,3h,\ldots\},h>0$h$h\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{(hk)^z}=h^{1-z}\zeta(z); h^{-z}=0 \mathrm{\hspace{2pt} or \hspace{2pt}} \mathrm{Re}(z)>1$$h^{-z}\zeta(z)$
$\{2,3,5,7,\ldots\}=\{p_1,p_2,\ldots\}$ (prime numbers)$\mu(p_n)=p_{n+1}-p_n$$\displaystyle\sum_{k=1}^{\infty} \dfrac{p_{k+1}-p_k}{p_k^z}$$\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{p_k^z}$ (prime zeta function)
$\{1,2,3,5,8,13,\ldots\}=\{f_1,f_2,\ldots\}$ (Fibonacci numbers)$\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{f_k^z}=-\dfrac{1}{z} + \zeta_{\mathrm{Fib}}(z)$ (Fibonacci zeta function)
$\{\ldots,a_{-2},a_{-1}\}$ (zeros of Airy Ai, $a_{k-1} \lt a_k$) $\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{(a_{-k})^z}$ (almost the Airy zeta function)
$\{a_1,a_2,\ldots\}=\{|a_{-1}|,|a_{-2}|,\ldots\}$$\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{a_k^z}=\zeta_{\mathrm{Ai}}(z)$ (Airy zeta function)
Some big questions
  1. Can we express the region of convergence in a closed form for all time scales? Possibly this could be achieved using the minimal graininess function that appears on this page.
  2. Can we find Euler products for any of these? Can we find Euler products on any classes of time scales?
  3. In what sense can we investigate the time scale analogue of the Riemann hypothesis? Answering it for the quantum time scales is probably easy.
  4. Are there any other time scales that have closed form solutions?
  5. If we allow $\mathbb{T}=[1,\infty)$ in the definition, then $\zeta_{\mathbb{T}}$ does not exist because the integral defining it diverges. If we take any time scale $\hat{\mathbb{T}}$ of isolated points for which $\zeta_{\hat{\mathbb{T}}}$ exists and form the time scale $\tilde{\mathbb{T}}=\hat{\mathbb{T}} \cup [2,3]$, $\zeta_{\tilde{\mathbb{T}}}$ will probably converge. Can we classify the full set of time scales for which the $\zeta_{\mathbb{T}}$ exists for at least one $z \in \mathbb{C}$? How about those that exist "for all $z$ satisfying $F(\mathrm{Re}(z))>\alpha$ for some "nice" function $F$ and some $\alpha \in \mathbb{R}$?
  6. If $\mathbb{T}$ is a bounded time scale, is it true that $\zeta_{\mathbb{T}}$ is everywhere holomorphic (or maybe everywhere not on a branch cut)?


Experiments Related to Riemann Zeta
Taking $\mathbb{T}=\{0,1,2!,3!,4!,\ldots\}$, we get $$\tilde{\zeta}_{\mathbb{T}}(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{1}{(k!)^z}.$$ The following image shows the domain coloring of this image for $\mathrm{Re}(z)>0$:
Taking the $q$-calculus $\mathbb{T}=2^{\mathbb{N}_0}$ yields \[ \overline{\zeta}_{\mathbb{T}}(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{1}{(2^k)^z} = \dfrac{1}{2^z-1}\] with picture
It was then shown that the poles (i.e. "tips" of the structures in the image) are at points of the form $z=\dfrac{2n\pi i}{\ln(2)}$ for $n \in \mathbb{Z}$. Taking $\mathbb{T}$ to be an imaginary $q$-calculus $(1+i)^{\mathbb{N}_0}$ yields $$\tilde{\zeta}_{\mathbb{T}}(z) = \dfrac{1}{(1+i)^z-1}$$ with picture
whose poles occur at $z=\left( \dfrac{8\pi^2}{4\ln(2)^2+\pi^2} + i \dfrac{16\pi\ln(2)}{4\ln(2)^2+\pi^2} \right)n$ for $n \in \mathbb{Z}$.