Webpage of Dr. Tom Cuchta

Processing math: 100%

AMPS | THARC | KE8QZC | SFW | TSW | WW

Back to the class

Section 9.1 #29: Prove the identity

$\cos(x) - \cos^3(x) = \cos(x) \sin^2(x).$ Solution: Recall the Pythagorean identity

$\cos^2(x)+\sin^2(x)=1$ and rearrange it to say

$\cos^2(x)=1-\sin^2(x)$ . Start with the left and calculate

$\begin{array}{ll} \cos(x) - \cos^3(x) &= \cos(x)(1-\cos^2(x)) \\ &= \cos(x)\sin^2(x), \end{array}$ completing the proof.

$\blacksquare$

Section 9.1 #30: Prove the identity

$\cos(x)(\tan(x)-\sec(-x))=\sin(x)-1.$ Solution: Recall the "even property" of cosine, i.e.

$\cos(-x)=\cos(x)$ . Start with the left and calculate

$\begin{array}{ll} \cos(x)(\tan(x)-\sec(-x))=\sin(x)-1 &= \cos(x) \left( \dfrac{\sin(x)}{\cos(x)} - \dfrac{1}{\cos(-x)} \right) = \sin(x)-1 \\ &= \cos(x) \left( \dfrac{\sin(x)}{\cos(x)} - \dfrac{1}{\cos(x)} \right) \\ &=\cos(x) \left( \dfrac{\sin(x)-1}{\cos(x)} \right) \\ &= \sin(x)-1, \end{array}$ completing the proof.

$\blacksquare$

Section 9.1 #33: Prove the identtiy

$\cos^2(x) - \tan^2(x) = 2-\sin^2(x)-\sec^2(x).$ Solution: Recall from the Pythagorean identity

$\cos^2(x)+\sin^2(x)=1$ we may conclude both

$1-\sin^2(x)=\cos^2(x)$ and

$\cos^2(x)-1=-\sin^2(x)$ . Start with the right and calculate

$\begin{array}{ll} 2-\sin^2(x)-\sec^2(x) &= 2 - \sin^2(x) - \dfrac{1}{\cos^2(x)} \\ &= (1-\sin^2(x)) + 1 - \dfrac{1}{\cos^2(x)} \\ &= \cos^2(x) + \dfrac{\cos^2(x)-1}{\cos^2(x)} \\ &= \cos^2(x) + \dfrac{-\sin^2(x)}{\cos^2(x)} \\ &= \cos^2(x) - \tan^2(x), \end{array}$ completing the proof.

$\blacksquare$

Section 9.1 #34: Prove or disprove whether or not the following equation is an identity:

$\dfrac{1}{1+\cos(x)} - \dfrac{1}{1-\cos(-x)} = -2\cot(x)\csc(x).$ Solution: Let us try a couple test values. First try

$x=\dfrac{\pi}{6}$ : calculate the left-hand side

$\dfrac{1}{1+\cos(\frac{\pi}{6})} - \frac{1}{1-\cos(-\frac{\pi}{6})} = \dfrac{1}{1+\frac{\sqrt{3}}{2}} - \dfrac{1}{1-\frac{\sqrt{3}}{2}} = -4\sqrt{3},$ now calculate the right-hand side

$-2 \cot \left( \dfrac{\pi}{6} \right) \csc \left( \dfrac{\pi}{6} \right) = ... = -4\sqrt{3}.$ They match. Now try a different value, say,

$x=\dfrac{\pi}{3}$ (you will find that it works ok). So now try to prove it as an identity: start with the left and compute

$\begin{array}{ll} \dfrac{1}{1+\cos(x)} - \dfrac{1}{1-\cos(-x)} &= \dfrac{(1-\cos(-x))-(1+\cos(x))}{(1+\cos(x))(1-\cos(-x))} \\ &=\dfrac{-2\cos(x)}{1-\cos^2(x)} \\ &= \dfrac{-2\cos(x)}{\sin^2(x)} \\ &= -2 \left( \dfrac{\cos(x)}{\sin(x)} \right) \left( \dfrac{1}{\sin(x)} \right) \\ &= -2\cot(x)\csc(x), \end{array}$ completing the proof.

$\blacksquare$

Section 9.1 #37: Prove or disprove whether the following equation is an identity:

$\dfrac{\tan(x)}{\sec(x)} \sin(-x) = \cos^2(x).$ Solution: Test a value for

$x$ , say

$x=\dfrac{\pi}{4}$ . Plugging this in for

$x$ in the left-hand side yields

$\dfrac{\tan(\frac{\pi}{4})}{\sec(\frac{\pi}{4})} \sin \left( - \dfrac{\pi}{4} \right) = \dfrac{1}{\frac{2}{\sqrt{2}}} \left( - \dfrac{\sqrt{2}}{2} \right) = -\dfrac{1}{2}.$ Now substitute

$x=\dfrac{\pi}{4}$ into the right-hand side yielding

$\cos^2 \left( \dfrac{\pi}{4} \right) = \left( \dfrac{\sqrt{2}}{2} \right)^2 = \dfrac{2}{4} = \dfrac{1}{2}.$ Since

$-\dfrac{1}{2} \neq \dfrac{1}{2}$ , we must conclude that the given equation is not and identity.

Section 9.2 #7: Find the exact value of

$\cos \left( \dfrac{11\pi}{12} \right)$ . Solution: Note that

$\dfrac{\pi}{6} + \dfrac{3\pi}{4} = \dfrac{2\pi}{12} + \dfrac{9\pi}{12} = \dfrac{11\pi}{12}.$ Therefore we may apply the sum identity for cosine, i.e.

$\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)$ with

$\alpha=\dfrac{\pi}{6}$ and

$\beta = \dfrac{3\pi}{4}$ to compute

$\begin{array}{ll} \cos \left( \dfrac{11\pi}{12} \right) &= \cos \left( \dfrac{\pi}{6} + \dfrac{3\pi}{4} \right) \\ &= \cos \left( \dfrac{\pi}{6} \right) \cos \left( \dfrac{3\pi}{4} \right) - \sin \left( \dfrac{\pi}{6} \right) \sin \left( \dfrac{3\pi}{4} \right) \\ &= \left( \dfrac{\sqrt{3}}{2} \right) \left( -\dfrac{\sqrt{2}}{2} \right) - \left( \dfrac{1}{2} \right) \left( \dfrac{\sqrt{2}}{2} \right) \\ &=\dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{array}$

Section 9.2 #11: Rewrite in terms of

$\sin(x)$ and

$\cos(x)$ :

$\sin \left( x - \dfrac{3\pi}{4} \right).$ Solution: Using the difference identity for sine, i.e.

$\sin(\alpha-\beta)=\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)$ with

$\alpha=x$ and

$\beta=\dfrac{3\pi}{4}$ , we write

$\begin{array}{ll} \sin \left( x - \dfrac{3\pi}{4} \right) &= \sin(x) \cos \left( - \dfrac{3\pi}{4} \right) - \cos(x) \sin \left( -\dfrac{3\pi}{4} \right) \\ &= -\dfrac{\sqrt{2}}{2} \sin(x) + \dfrac{\sqrt{2}}{2} \cos(x). \end{array}$

Section 9.2 #16: Simplify the expression

$\cot \left( \dfrac{\pi}{2} - x \right)$ .
Solution: Recall the difference identity for sine (in previous problem) and the difference identity for cosine:

$\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)$ with

$\alpha=\dfrac{\pi}{2}$ and

$\beta=x$ . Write

$\begin{array}{ll} \cot \left( \dfrac{\pi}{2} - x \right) &= \dfrac{\cos( \frac{\pi}{2}-x)}{\sin(\frac{\pi}{2} - x )} \\ &=\dfrac{\cos(\frac{\pi}{2})\cos(x) + \sin(\frac{\pi}{2})\sin(x)}{\sin(\frac{\pi}{2})\cos(x)-\cos(\frac{\pi}{2})\sin(x)} \\ &= \dfrac{0 \cdot \cos(x) + 1 \cdot \sin(x)}{1 \cdot \cos(x) - 0 \cdot \sin(x)} \\ &= \dfrac{\sin(x)}{\cos(x)} \\ &= \tan(x). \end{array}$

Section 9.2 #18: Simplify the expression

$\sin(2x)\cos(5x) - \sin(5x)\cos(2x).$ Solution: Recall the difference identity for sine (earlier). The expression in this problem looks like the right-hand side of th diffrence identity for sine with

$\alpha=2x$ and

$\beta=5x$ . Therefore we see that

$\begin{array}{ll} \sin(2x)\cos(5x) - \sin(5x)\cos(2x) &= \sin(2x-5x) \\ &= \sin(-3x) \\ &= -\sin(3x). \end{array}$

Section 9.2 #20: Given that

$\sin(a) = \dfrac{2}{3}$ and

$\cos(b)=-\dfrac{1}{4}$ , with

$a$ and

$b$ both in the interval

$\left[ \dfrac{\pi}{2}, \pi \right)$ , find

$\sin(a+b)$ and

$\cos(a-b)$ .
Solution: Note that

$a$ and

$b$ are both in quadrant II. First we will find

$\sin(b)$ and

$\cos(a)$ . To find

$\sin(b)$ consider the following triangle that agrees with

$\sin(a)=\dfrac{2}{3}$ :

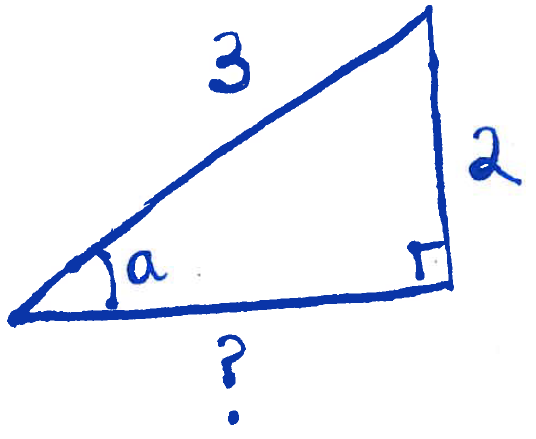and find the missing side labelled "

$?$ ". To do that, use the Pythagorean theorem to write

$?^2+2^2=3^2,$ yielding

$?=\sqrt{5}$ . Therefore

$\cos(a)=-\dfrac{\sqrt{5}}{4}$ . To find

$\cos(a)$ consider the following triangle:

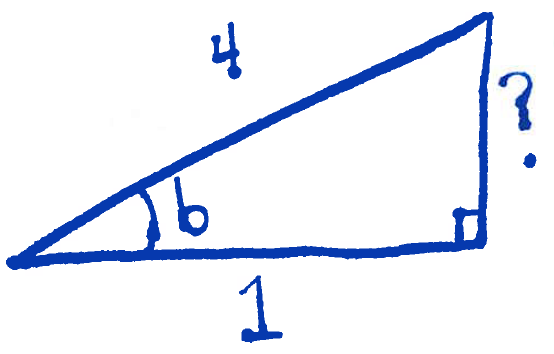and find the missing side labelled "

$?$ ". To do that, use the Pythagorean theorem to write

$1^2+?^2 = 4^2,$ yielding

$?=\sqrt{15}$ . Therefore

$\sin(b)=\dfrac{\sqrt{15}}{4}$ (note that sine is positive in quadrant II). Using the sum and difference identities, we compute

$\begin{array}{ll} \sin(a+b) &= \sin(a)\cos(b)+\cos(a)\sin(b) \\ &= \left( \dfrac{2}{3} \right) \left( - \dfrac{1}{4} \right) + \left( -\dfrac{\sqrt{5}}{4} \right) \left( \dfrac{\sqrt{15}}{4} \right). \end{array}$ and we compute

$\begin{array}{ll} \cos(a-b) &= \cos(a)\cos(b) + \sin(a)\sin(b) \\ &= \left( - \dfrac{\sqrt{5}}{4} \right) \left(-\dfrac{1}{4} \right) + \left( \dfrac{2}{3} \right) \left( \dfrac{\sqrt{15}}{4} \right). \end{array}$

Section 9.2 #23: Find the exact value of

$\cos \left( \cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) + \sin^{-1}\left( \dfrac{\sqrt{3}}{2} \right) \right) .$ Solution: Recall that

$\cos^{-1}$ outputs an angle in the range

$[0,\pi]$ and

$\sin^{-1}$ outputs an angle in the range

$\left[ - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right]$ . Therefore

$\cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}$ and

$\sin^{-1} \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{3}.$ Now applying the sum identity for cosine yields

$\begin{array}{ll} \cos \left( \cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) + \sin^{-1} \left( \dfrac{\sqrt{3}}{2} \right) \right) &= \cos \left( \dfrac{\pi}{4} + \dfrac{\pi}{3} \right) \\ &= \cos \left( \dfrac{\pi}{4} \right) \cos \left( \dfrac{\pi}{3} \right) - \sin\left( \dfrac{\pi}{4} \right) \sin \left( \dfrac{\pi}{3} \right) \\ &=\left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{1}{2} \right) - \left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{\sqrt{3}}{2} \right). \end{array}$

Section 9.1 #51: Prove the identity

$\dfrac{\cos(x+h)-\cos(x)}{h} = \cos(x) \dfrac{\cos(h)-1}{h} - \sin(x) \dfrac{\sin(h)}{h}.$ Solution: Using the sum identity for cosine, compute

$\begin{array}{ll} \dfrac{\cos(x+h)-\cos(x)}{h} &= \dfrac{(\cos(x)\cos(h)-\sin(x)\sin(h))-\cos(x)}{h} \\ &= \dfrac{\cos(x)\cos(h)-\cos(x)}{h} - \sin(x) \dfrac{\sin(h)}{h} \\ &= \cos(x) \dfrac{\cos(h)-1}{h} - \sin(x) \dfrac{\sin(h)}{h}. \end{array}$