Return to the class
Homework 2
Section 7.1 #24) Find the arc length indicated in the following image:
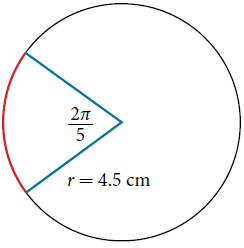
Solution: Recall the fundamental relationship: $s=r\theta$, where $s$ denotes arc length, $r$ denotes the radius, and $\theta$ the (radian) measure of the angle. In this problem, we are told $r=4.5$ and $\theta=\dfrac{2\pi}{5}$ and are asked to find $s$. Therefore
$$s = (4.5)\dfrac{2\pi}{5} = \dfrac{9\pi}{5} \approx 5.65 \mathrm{cm}.$$
Section 7.1 #27) Convert to degree measure: $\dfrac{\pi}{9}$ radians.
Solution: Recall that $180^{\circ}=\pi \hspace{2pt} \mathrm{radians}$ so that $\dfrac{180^{\circ}}{\pi \hspace{2pt} \mathrm{radians}} = 1$. Therefore compute
$$\begin{array}{ll}
\dfrac{\pi}{9} \hspace{2pt} \mathrm{radians} &= \left( \dfrac{\pi}{9} \hspace{2pt} \mathrm{radians} \right) (1) \\
&= \left( \dfrac{\pi}{9} \hspace{2pt} \mathrm{radians} \right) \left( \dfrac{180^{\circ}}{\pi \hspace{2pt} \mathrm{radians}} \right) \\
&= \left( \dfrac{180}{9} \right)^{\circ} \\
&= 20^{\circ}.
\end{array}$$
Section 7.1 #28) Convert $-\dfrac{5\pi}{4}$ radians to degrees.
Solution: Calculate
$$-\dfrac{5\pi}{4} \mathrm{\hspace{2pt} rad} = \left( -\dfrac{5\pi}{4} \mathrm{\hspace{2pt} rad} \right)\left( \dfrac{360^{\circ}}{2\pi \mathrm{\hspace{2pt} rad}} \right) = -\left( \dfrac{5(360)}{2(4)} \right)^{\circ}=-225^{\circ}.$$
Section 7.1 #35) Convert $-540^{\circ}$ to radians.
Solution: Calculate
$$-540^{\circ}= \left( -540^{\circ} \right) \left( \dfrac{2\pi \mathrm{\hspace{2pt} rad}}{360^{\circ}} \right)=-\dfrac{540(2\pi)}{360} \mathrm{\hspace{2pt} rad}=-3\pi \mathrm{\hspace{2pt} rad}.$$
Section 7.1 #43) Find the length of the arc of a circle of radius $10$ centimeters subtended by the central angle of $50^{\circ}$.
Solution: Recall the fundamental relationship $s=r\theta$ ($\theta$ must be in radians!!!!). In this problem we are told $r=10$ and $\theta=50^{\circ}$. First convert $50^{\circ}$ into radians:
$$50^{\circ} = \left( 50^{\circ} \right) \left( \dfrac{\pi \hspace{2pt} \mathrm{radians}}{180^{\circ}} \right) = \dfrac{5\pi}{18} \mathrm{radians}.$$
With these values, we see that the desired arc length, $s$, is
$$s = 10 \left( \dfrac{5\pi}{18} \right) = \dfrac{50\pi}{18} \approx 8.73.$$
Section 7.2 #12: Find the missing sides if side $a$ is opposide angle $A$, side $b$ is opposite angle $B$, and side $c$ is the hypotenuse:
$$\tan A = \dfrac{5}{12}, b=6.$$
Solution: First draw the described triangle:
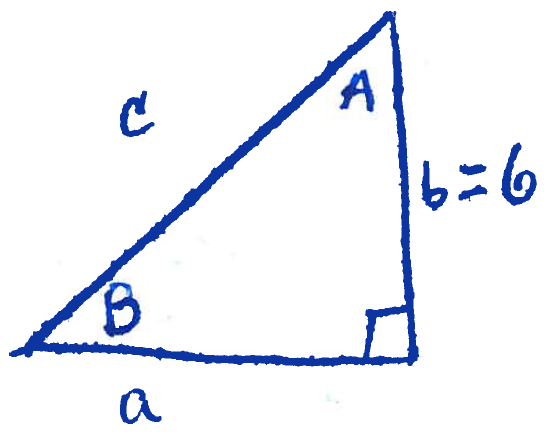By definition, $\tan(A)=\dfrac{a}{b}=\dfrac{a}{6}$ by what we are told. However we are also told that $\tan(A) = \dfrac{5}{12}$. To find $a$ equate these two to see that
$$\dfrac{5}{12} = \tan(A) = \dfrac{a}{6},$$
and solve for $a$ by multiplying by $6$ to get $a = 6\dfrac{5}{12} = \dfrac{5}{2}$. To find the hypotenuse $c$, the Pythagorean theorem tells us that
$$a^2+b^2=c^2,$$
so plug in $a$ and $b$ to get
$$\left( \dfrac{5}{2} \right)^2 + 6^2 = c^2,$$
and simplify the left-hand side to get
$$\dfrac{25}{4} + 36 = c^2,$$
or equivalently
$$\dfrac{25+144}{4} = c^2,$$
or
$$\dfrac{169}{4}=c^2,$$
so that the hypotenuse is
$$c = \sqrt{ \dfrac{169}{4} } = \dfrac{\sqrt{169}}{\sqrt{4}} = \dfrac{13}{2}.$$
(note: we ignored the negative solution because we are solving for the leg of a triangle, a length, which cannot be negative!)
Section 7.2 #17: Find $\sin(A)$ in the following picture:
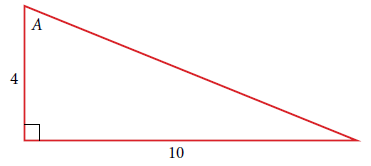
Solution: To find $\sin(A)$ we need to know the length of the hypotenuse. To find that, use the Pythagorean theorem to write
$$10^2+4^2=\mathrm{hyp}^2.$$
Simplifying on the left yields $116=\mathrm{hyp}^2$, so $\mathrm{hyp}=\sqrt{116}$ (we ignore the negative solution to this equation because it is not physically meaningful). Therefore we may now compute
$$\sin(A) = \dfrac{\mathrm{opposite \hspace{2pt} of \hspace{2pt}} A}{\mathrm{hypotenuse}} = \dfrac{10}{\sqrt{116}}.$$
Section 7.2 #31: Solve for the unknown sides of the following triangle:
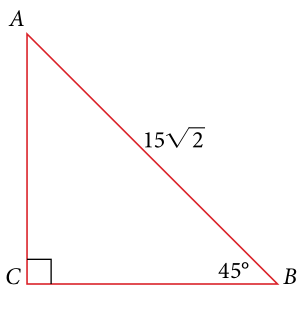
Solution:
Solve for side opposite the $45^{\circ}$ angle
Call this side $b$. We see that $\sin(45^{\circ})=\dfrac{b}{15\sqrt{2}}$ and so solving for $b$ yields $b=15\sqrt{2}\sin(45^{\circ})$.
Solve for side opposite of angle $A$
Call this side $a$. We see that $\cos(45^{\circ})=\dfrac{a}{15\sqrt{2}}$ and so solving this for $a$ yields $a=15\sqrt{2}\cos(45^{\circ})$.
Section 7.2 #51: There is a lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be $36^{\circ}$. From the same location, the angle of elevation to the top of the lightning rod is measured to be $38^{\circ}$. Find the height of the lightning rod.
Solution: Draw this problem, labelling the height of the building as $h_B$ and the height of the lightning rod as $h_L$:
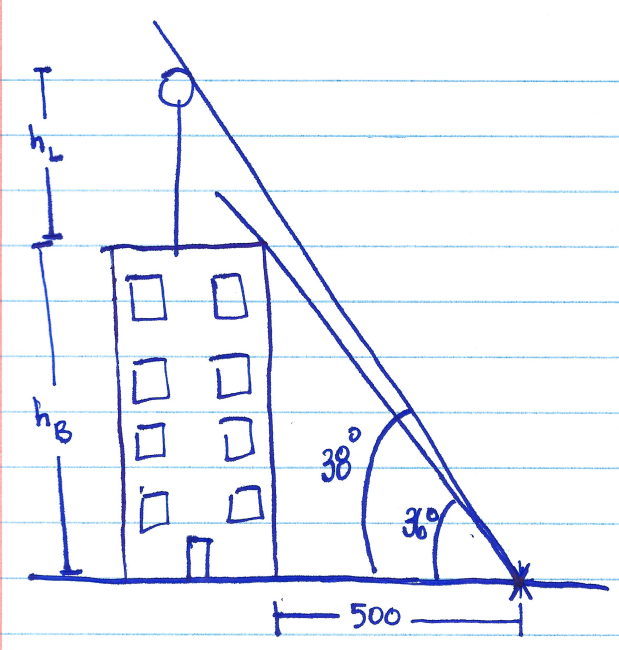
There are two natural triangles to work with that appear in the image:
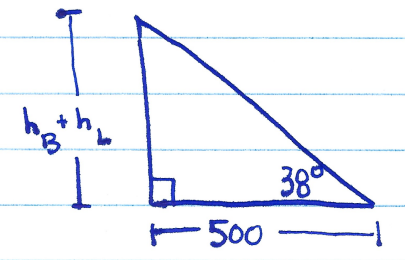
and
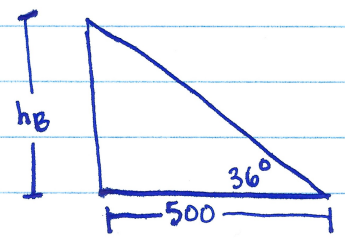
In the first of those two triangles, we use the tangent function to write
$$\tan(38^{\circ}) = \dfrac{h_B+h_L}{500}.$$
Solving for $h_B+h_L$ yields $h_B+h_L=500\tan(38^{\circ})$. In the second of the two triangles, we use the tangent function to write
$$\tan(36^{\circ})=\dfrac{h_B}{500}.$$
Solving for $h_B$ yields $h_B=500\tan(36^{\circ})$. We would like to solve for $h_L$. Since $(h_B+h_L)-h_B=h_L$, this shows us that
$$h_L = (h_B+h_L)-h_b = 500\tan(38^{\circ}) - 500\tan(36^{\circ}) \approx 27.37 \mathrm{\hspace{2pt} feet}.$$
