Return to the class
Homework 1
Section 2.2 #6: Solve $7x+2=3x-9$.
Solution: Subtract $3x$ to get $4x+2=-9$. Subtract $2$ to get $4x=-11$. Divide by $4$ to get $x = -\dfrac{11}{4}$.
Section 2.2 #7: Solve $4x-3=5$.
Solution: Add $3$ to get $4x=8$. Divide by $4$ to get $x=2$.
Section 2.2 #8: Solve $3(x+2)-12=5(x+1)$.
Solution: Distribute the $3$ on the left and the $5$ on the right to get $3x+6-12=5x+5$. Simplify the arithmetic on the left to get $3x-6=5x+5$. Add $6$ to get $3x=5x+11$. Subtract $5x$ to get $-2x=11$. Divide by $-2$ to get $x=-\dfrac{11}{2}$.
Section 2.5 #8: Solve by factoring: $2x^2+9x-5=0$.
Solution: The left-hand side factors as
$$(2x-1)(x+5)=0.$$
This means $2x-1=0$ or $x+5=0$. Solving each of these yields $x=\dfrac{1}{2}$ and $x=-5$.
Section 2.5 #19: Solve the equation $x^2=36$.
Solution: Taking square roots of each side yields $x=\pm \sqrt{36} = \pm 6$.
Section 2.5 #38: Solve $2x^2+5x+3=0$.
Solution: It is not clear how to factor this. Therefore apply the quadratic formula to get
$$x=\dfrac{-5 \pm \sqrt{25-4(2)(3)}}{2(2)} = \dfrac{-5 \pm \sqrt{1}}{4} = \dfrac{-5 \pm 1}{4}.$$
Therefore the solutions are $x=\dfrac{-4}{4}=-1$ and $x=\dfrac{-6}{4}=-\dfrac{3}{2}$.
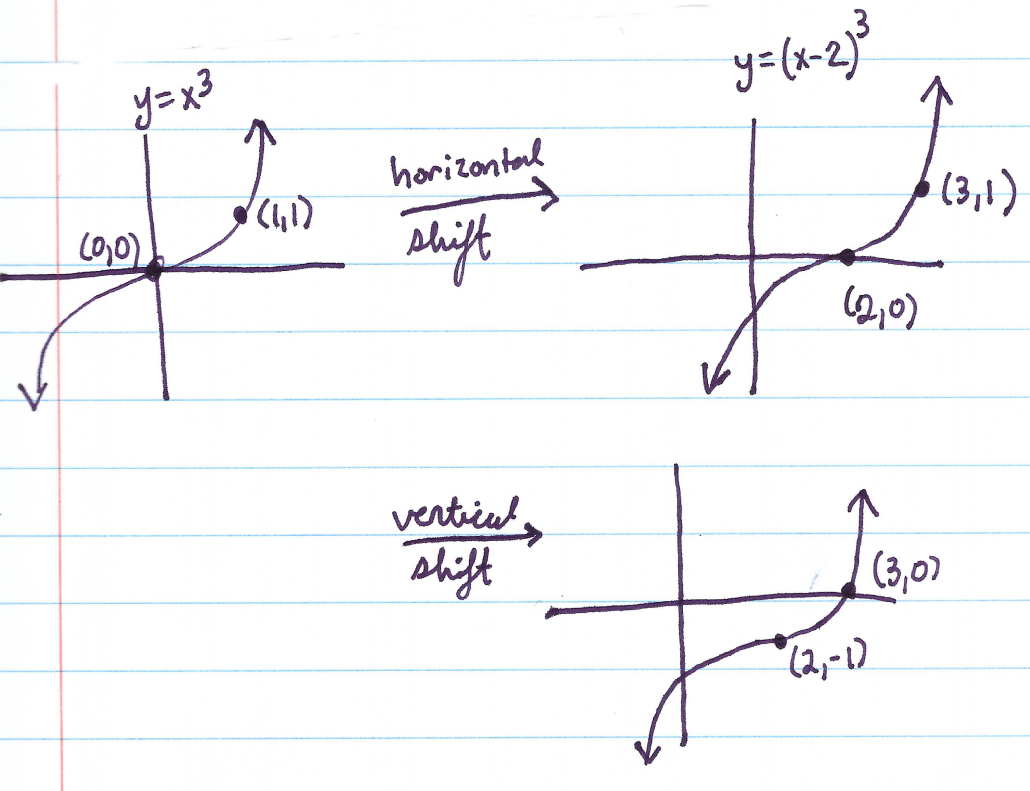
Section 3.5 #29: Sketch the graph of $k(x)=(x-2)^3-1$
Solution: Notice that there is a horizontal shift to the right by $2$ and a vertical shift down by $1$. Draw it in the following way:
Section 7.1 #8: Draw an angle in standard position with the measure $-80^{\circ}$.
Solution:

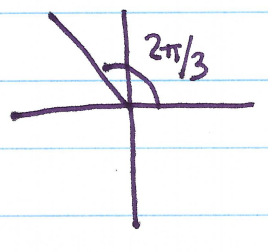
Section 7.1 #11: Draw an angle in standard position with the measure $\dfrac{2\pi}{3}$.
Solution: