Back to the class
Homework 9
Section 8.5 #5: Compute $\displaystyle\int \dfrac{1}{x^2-9} \mathrm{d}x$.
Solution: First factor the denominator:
$$x^2-9=(x-3)(x+3).$$
Now set up the partial fractions calculation:
$$\dfrac{1}{x^2-9} = \dfrac{A}{x-3} + \dfrac{B}{x+3}.$$
Multiply both sides by $x^2-9$ to get
$$1 = A(x+3) + B(x-3) = (A+B)x + (3A-3B).$$
Equating coefficients yields the following system of equations:
$$\left\{ \begin{array}{lll}
A+B &= 0 & (i)\\
3A-3B &= 1 & (ii)
\end{array} \right.$$
From equation $(i)$, we get $A=-B$ and plugging this into equation $(ii)$ yields $3(-B)-3B=1$, or $-6B=1$, or $B=-\dfrac{1}{6}$. Using this value of $B$ and our previous formula for $A$, we get $A = -B=- \left( -\dfrac{1}{6} \right)=\dfrac{1}{6}$. Therefore we have shown
$$\dfrac{1}{x^2-9} = \dfrac{1}{6(x-3)} - \dfrac{1}{6(x+3)}.$$
Therefore we may compute
$$\begin{array}{ll}
\displaystyle\int \dfrac{1}{x^2-9} \mathrm{d}x &= \dfrac{1}{6} \displaystyle\int \dfrac{1}{x-3} \mathrm{d}x - \dfrac{1}{6} \displaystyle\int \dfrac{1}{x+3} \mathrm{d}x \\
&= \dfrac{1}{6} \ln(|x-3|) - \dfrac{1}{6} \ln(|x+3|) + C.
\end{array}$$
Section 8.5, #11: Compute $\displaystyle\int \dfrac{2x^3-4x^2-15x+5}{x^2-2x-8} \mathrm{d}x$.
Solution: First, the degree of the numerator is greater than the degree of the denominator, so we will have to do polynomial long division:
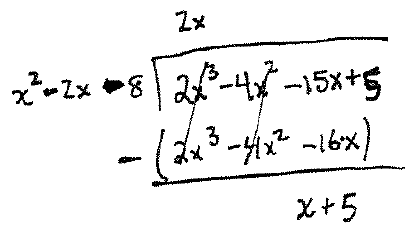
This shows that
$$\dfrac{2x^3-4x^2-15x+5}{x^2-2x-8} = 2x + \dfrac{x+5}{x^2-2x-8}.$$
Since $(x^2-2x-8)=(x-4)(x+2)$, we will write
$$\dfrac{x+5}{(x-4)(x+2)} = \dfrac{A}{x-4} + \dfrac{B}{x+2}.$$
Multiply by the common denominator to get
$$x+5 = A(x+2) + B(x-4) = (A+B)x + (2A-4B).$$
Equating coefficients yields the system
$$\left\{ \begin{array}{lll}
A+B &= 1 & (i) \\
2A-4B &= 5 & (ii)
\end{array} \right.$$
Solve $(i)$ for $A$ to get $B=1-A$ and plug this into $(ii)$ to get $2A-4(1-A)=5$, or $6A-4=5$, or $6A=9$, or $A = \dfrac{9}{6}=\dfrac{3}{2}$. Now plug this into our formula for $B$ to get $B=1-\dfrac{3}{2}=-\dfrac{1}{2}$. We have now shown
$$\dfrac{x+5}{(x-4)(x+2)} = \dfrac{3}{2} \dfrac{1}{x-4} - \dfrac{1}{2} \dfrac{1}{x+2}.$$
Therefore compute
$$\begin{array}{ll}
\displaystyle\int \dfrac{2x^3-4x^2-15x+5}{x^2-2x-8} \mathrm{d}x &= \displaystyle\int 2x \mathrm{d}x + \dfrac{3}{2} \displaystyle\int \dfrac{1}{x-4} \mathrm{d}x -\dfrac{1}{2} \displaystyle\int \dfrac{1}{x+2} \mathrm{d}x \\
&= x^2 + \dfrac{3}{2} \ln(|x-4|) - \dfrac{1}{2} \ln(|x+2|) + C.
\end{array}$$
Section 8.7, #19 Compute $\displaystyle\lim_{x \rightarrow 0} \dfrac{\sin(3x)}{\sin(5x)}.$
Solution: Since $\sin(0)=0$, naively plugging in $x=0$ yields indeterminate form $\dfrac{0}{0}$, so L'Hopital's rule will apply. So use it to compute
$$\begin{array}{ll}
\displaystyle\lim_{x \rightarrow 0} \dfrac{\sin(3x)}{\sin(5x)} &\stackrel{L.H.}{=} \displaystyle\lim_{x \rightarrow 0} \dfrac{3\cos(3x)}{5\cos(5x)} \\
&= \dfrac{3}{5},
\end{array}$$
since $\cos(0)=1$.
Section 8.7, #27: Compute $\displaystyle\lim_{x \rightarrow \infty} \dfrac{x^3}{e^{\frac{x}{2}}}.$
Solution: Naively plugging in $x=\infty$ yields the indeterminate form $\dfrac{\infty}{\infty}$, so L'Hopital's rule will apply (also this will happen numerous times in the succeeding calculation). So compute
$$\begin{array}{ll}
\displaystyle\lim_{x \rightarrow \infty} \dfrac{x^3}{e^{\frac{x}{2}}} &\stackrel{L.H.}{=} \displaystyle\lim_{x \rightarrow \infty} \dfrac{3x^2}{\frac{1}{2}e^{\frac{x}{2}}} \\
&\stackrel{L.H.}{=} \displaystyle\lim_{x \rightarrow \infty} \dfrac{6x}{\frac{1}{4}e^{\frac{x}{2}}} \\
&\stackrel{L.H.}{=} \displaystyle\lim_{x \rightarrow \infty} \dfrac{6}{\frac{1}{8}e^{\frac{x}{2}}} \\
&=0,
\end{array}$$
since the exponential approaches $\infty$ as $x$ gets large.
Section 8.8 #18: Calculate $\displaystyle\int_1^{\infty} \dfrac{6}{x^4} \mathrm{d}x$.
Solution: We calculate
$$\begin{array}{ll}
\displaystyle\int_1^{\infty} \dfrac{6}{x^4} \mathrm{d}x &= 6 \displaystyle\lim_{b \rightarrow \infty} \displaystyle\int_1^b x^{-4} \mathrm{d}x \\
&=6 \displaystyle\lim_{b \rightarrow \infty} \dfrac{x^{-3}}{-3} \Bigg|_1^b \\
&=-2 \displaystyle\lim_{b \rightarrow \infty} \left(\dfrac{1}{b^3} - 1 \right) \\
&=-2(-1) \\
&=2.
\end{array}$$
Section 8.8 #21: Calculate $\displaystyle\int_{-\infty}^0 xe^{-4x} \mathrm{d}x$.
Solution: We will use integration by parts with $u=x$ and $\mathrm{d}v=e^{-4x} \mathrm{d}x$ so that $\mathrm{d}u=\mathrm{d}x$ and $v=-\dfrac{1}{4}e^{-4x}$. So calculate
$$\begin{array}{ll}
\displaystyle\int_{-\infty}^0 xe^{-4x} \mathrm{d}x &= \displaystyle\lim_{a \rightarrow -\infty} \displaystyle\int_a^0 x e^{-4x} \mathrm{d}x \\
&= \displaystyle\lim_{a \rightarrow -\infty} \left[ -\dfrac{x}{4}e^{-4x} \Bigg|_a^0 + \dfrac{1}{4} \displaystyle\int_a^0 e^{-4x} \mathrm{d}x \right] \\
&=\displaystyle\lim_{a \rightarrow -\infty} \left[ \dfrac{a}{4}e^{-4a} - \dfrac{1}{16} (1-e^{-4a}) \right],
\end{array}$$
but this limit does not converge because
$$\displaystyle\lim_{a \rightarrow -\infty} e^{-4a} \stackrel{\mathrm{same \hspace{2pt} as}}{=} \displaystyle\lim_{w \rightarrow \infty} e^{4w} = \infty.$$