Back to the class
Homework 8 Problems
Section 8.3 problems
1. Find $\displaystyle\int \cos^3(x)\sin^2(x) \mathrm{d}x$.
Solution: Since the power of cosine is odd, write
$$\cos^3(x)=\cos(x) (1-\sin^2(x)),$$
so
$$\begin{array}{ll}
\displaystyle\int \cos^3(x)\sin^2(x) \mathrm{d}x &= \displaystyle\int \cos(x) (1-\sin^2(x))\sin^2(x) \mathrm{d}x \\
&\stackrel{u=\sin(x)} = \displaystyle\int (1-u^2)u^2 \mathrm{d}u \\
&= \displaystyle\int u^2 \mathrm{d}u - \displaystyle\int u^4 \mathrm{d}u \\
&= \dfrac{u^3}{3} - \dfrac{u^5}{5} + C \\
&= \dfrac{\sin^3(x)}{3} - \dfrac{\sin^5(x)}{5} + C.
\end{array}$$
Note: using WolframAlpha on this yields $\dfrac{\sin^3(x)}{30}(3\cos(2x)+7)$, which is equivalent to our solution.
2. Find $\displaystyle\int \sin^3(2\theta) \sqrt{\cos(2\theta)} \mathrm{d}\theta$.
Solution: Since the power of sine is odd, write
$$\sin^3(2\theta)=\sin(2\theta)\sin^2(2\theta)=\sin(2\theta)(1-\cos^2(2\theta)),$$
so
$$\begin{array}{ll}
\displaystyle\int \sin^3(2\theta) \sqrt{\cos(2\theta)} \mathrm{d}\theta &= \displaystyle\int \sin(2\theta) \left( 1-\cos^2(2\theta) \right) (\cos(2\theta))^{\frac{1}{2}} \mathrm{d}\theta \\
&\stackrel{u=\cos(2\theta)}{=} -\dfrac{1}{2} \displaystyle\int (1-u^2)u^{\frac{1}{2}} \mathrm{d}u \\
&= -\dfrac{1}{2} \left[ \dfrac{u^{\frac{3}{2}}}{\frac{3}{2}} - \dfrac{u^{\frac{7}{2}}}{\frac{7}{2}} \right] + C \\
&=-\dfrac{1}{3} \cos^{\frac{3}{2}}(2\theta) + \dfrac{1}{7} \cos^{\frac{7}{2}}(2\theta) + C.
\end{array}$$
3. Find $\displaystyle\int \sin^4(x)\cos^2(x)\mathrm{d}x$.
Solution: We use the identities
$$\sin^2(\theta)=\dfrac{1-\cos(2\theta)}{2}$$
and
$$\cos^2(\theta)=\dfrac{1+\cos(2\theta)}{2}$$
to write
$$\sin^4(x) = (\sin^2(x))^2=\left( \dfrac{1-\cos(2x)}{2} \right)^2=\dfrac{1-2\cos(2x)+\cos^2(2x)}{4},$$
yielding
$$(*) \hspace{35pt} \begin{array}{ll}
\displaystyle\int \sin^4(x)\cos^2(x) \mathrm{d}x &= \displaystyle\int \left( \dfrac{1-2\cos(2x)+\cos^2(2x)}{4} \right) \left( \dfrac{1+\cos(2x)}{2} \right) \mathrm{d}x \\
&=\dfrac{1}{8} \displaystyle\int (1-2\cos(2x)+\cos^2(2x)) + (\cos(2x)-2\cos^2(2x)+\cos^3(2x)) \mathrm{d}x \\
&=\dfrac{1}{8} \displaystyle\int 1 -\cos(2x) -\cos^2(2x) +\cos^3(2x) \mathrm{d}x \\
&=\dfrac{1}{8} \left[ x - \dfrac{1}{2}\sin(2x) \right] + \dfrac{1}{8} \displaystyle\int \cos^3(2x)-\cos^2(2x) \mathrm{d}x \\
\end{array}$$
To evaluate the remaining two integrals, we will use the trig identity to rewrite
$$\cos^2(2x)=\dfrac{1+\cos(4x)}{2},$$
and we will write
$$\cos^3(2x)=\cos(2x)(1-\sin^2(2x)),$$
yielding from (*):
$$\begin{array}{ll}
\displaystyle\int \sin^4(x)\cos^2(x) \mathrm{d}x &= \dfrac{1}{8} \left[ x - \dfrac{1}{2}\sin(2x) \right] + \dfrac{1}{8} \displaystyle\int \cos^3(2x)-\cos^2(2x) \mathrm{d}x \\
&= \dfrac{1}{8} \left[ x - \dfrac{1}{2} \sin(2x) \right] + \dfrac{1}{8} \displaystyle\int (1-\sin^2(2x))\cos(2x) \mathrm{d}x - \dfrac{1}{8} \displaystyle\int \left( \dfrac{1+\cos(4x)}{2} \right) \mathrm{d}x \\
&\stackrel{u=\sin(2x)}{=} \dfrac{1}{8} \left[ x - \dfrac{1}{2} \sin(2x) \right] + \dfrac{-1}{16} \displaystyle\int 1-u^2 \mathrm{d}u - \dfrac{1}{16} \left[ x + \dfrac{1}{4} \sin(4x) \right] \\
&= \dfrac{1}{8} \left[ x - \dfrac{1}{2} \sin(2x) \right] - \dfrac{1}{16} \left[ u - \dfrac{u^3}{3} \right] - \dfrac{1}{16} \left[ x + \dfrac{1}{4} \sin(4x) \right] \\
&= \dfrac{1}{8} \left[ x - \dfrac{1}{2} \sin(2x) \right] - \dfrac{1}{16} \left[ \sin(2x) - \dfrac{\sin^3(2x)}{3} \right] - \dfrac{1}{16} \left[ x + \dfrac{1}{4} \sin(4x) \right] \\
&= \dfrac{x}{16} - \dfrac{1}{8} \sin(2x) + \dfrac{\sin^3(2x)}{48}-\dfrac{1}{64} \sin(4x)+C
\end{array}$$
4. Find $\displaystyle\int \tan^3(x)\sec^2(x) \mathrm{d}x$.
Solution: We will use the identity $\tan^2(\theta)+1=\sec^2(\theta)$ rewritten as $\tan^2(\theta)=\sec^2(\theta)-1$ to write
$$\begin{array}{ll}
\tan^3(x)\sec^2(x)&=\sec(x)\tan(x) \tan^2(x) \sec(x) \\
&= \sec(x)\tan(x) (\sec^2(x)-1)\sec(x) \\
&=\sec(x)\tan(x) (\sec^3(x)-\sec(x)).
\end{array}$$
Therefore we compute
$$\begin{array}{ll}
\displaystyle\int \tan^3(x)\sec^2(x) \mathrm{d}x &= \displaystyle\int \sec(x)\tan(x) \sec^3(x) \mathrm{d}x - \displaystyle\int \sec(x)\tan(x) \sec(x) \mathrm{d}x \\
&\stackrel{u=\sec(x)}{=} \displaystyle\int u^3 \mathrm{d}u - \displaystyle\int u \mathrm{d}u \\
&= \dfrac{u^4}{4} - \dfrac{u^2}{2} +C \\
&= \dfrac{\sec^4(x)}{4} - \dfrac{\sec^2(x)}{2} + C.
\end{array}$$
5. Find $\displaystyle\int \sec^4(x) \mathrm{d}x$.
Solution: We use the identity $\sec^2(\theta)=\tan^2(\theta)+1$ to write
$$\sec^4(x)=\sec^2(x)\sec^2(x)=\sec^2(x)(\tan^2(x)+1).$$
Now since $\displaystyle\int \sec^2(x) \mathrm{d}x = \tan(x)$, we compute
$$\begin{array}{ll}
\displaystyle\int \sec^4(x) \mathrm{d}x &= \displaystyle\int \sec^2(x) (\tan^2(x)+1) \mathrm{d}x \\
&= \displaystyle\int \sec^2(x) \tan^2(x) \mathrm{d}x + \displaystyle\int \sec^2(x) \mathrm{d}x \\
&\stackrel{u=\tan(x)}{=} \displaystyle\int u^2 \mathrm{d}u + \tan(x) + C \\
&= \dfrac{u^3}{3} + \tan(x) + C \\
&= \dfrac{\tan^3(x)}{3} + \tan(x) + C.
\end{array}$$
Section 8.4 problems
6. Find $\displaystyle\int \dfrac{4}{x^2\sqrt{16-x^2}} \mathrm{d}x$.
Solution: Let $x=4\sin(\theta)$ so that $\mathrm{d}x=4\cos(\theta) \mathrm{d}\theta$ and
$$\begin{array}{ll}
\dfrac{4}{x^2\sqrt{16-x^2}}&=\dfrac{4}{16\sin^2(\theta)\sqrt{16-16\sin^2(\theta)}} \\
&= \dfrac{1}{16\sin^2(\theta)\cos(\theta)}.
\end{array}$$
Therefore compute
$$(*) \hspace{35pt} \begin{array}{ll}
\displaystyle\int \dfrac{4}{x^2\sqrt{16-x^2}} \mathrm{d}x &= \displaystyle\int \dfrac{1}{16\sin^2(\theta)\cos(\theta)} 4\cos(\theta) \mathrm{d}\theta \\
&=\dfrac{1}{4} \displaystyle\int \dfrac{1}{\sin^2(\theta)} \mathrm{d}\theta \\
&= \dfrac{1}{4} \displaystyle\int \csc^2(\theta) \mathrm{d}\theta \\
&= -\dfrac{1}{4} \cot(\theta) + C
\end{array}$$
To finish, notice that our original assignment $x=4\sin(\theta)$ tells us that $\theta=\arccos\left( \dfrac{x}{4} \right)$ and $\cos(\theta)=\dfrac{x}{4}$, leading to the following triangle:
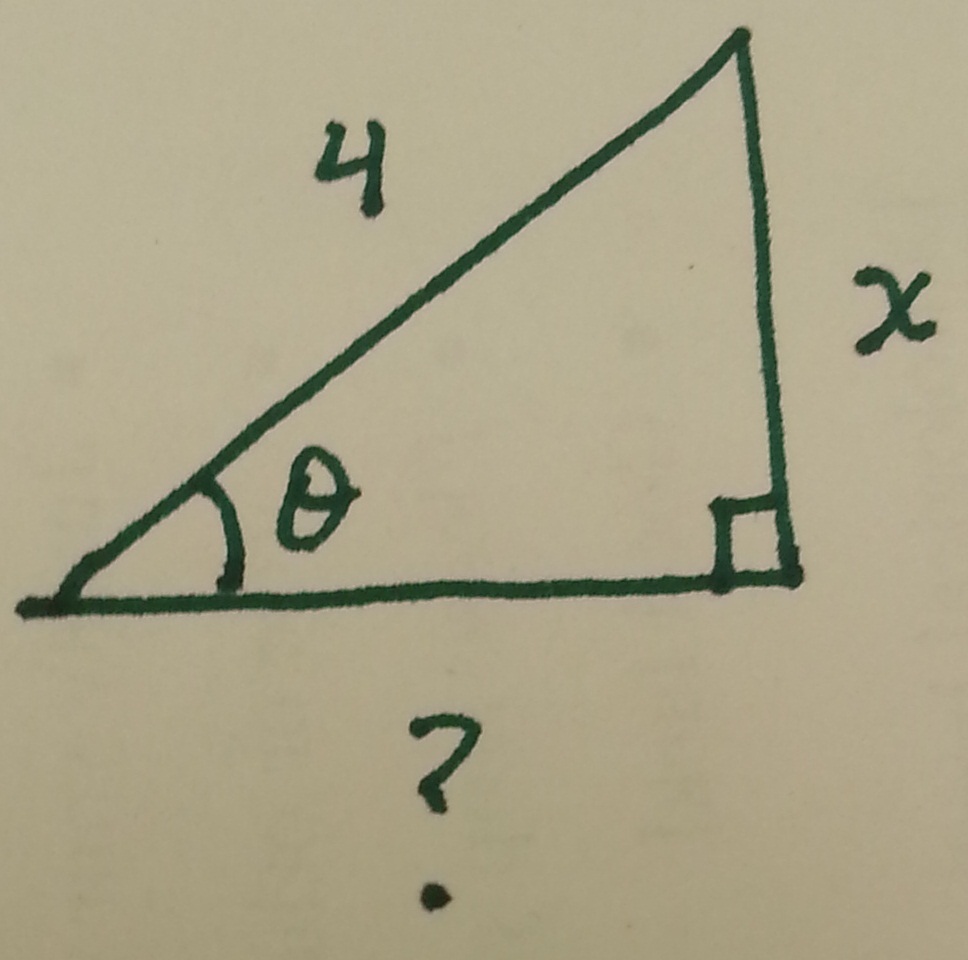
To find the missing side labelled "$?$", use the Pythagorean theorem to get
$$x^2+?^2 = 4^2,$$
or
$$? = \sqrt{16-x^2}.$$
Thus $\cot(\theta)=\dfrac{\sqrt{16-x^2}}{x}.$
Now from $(*)$ we see
$$\displaystyle\int \dfrac{4}{x^2\sqrt{16-x^2}} \mathrm{d}x = -\dfrac{1}{4}\cot(\theta) + C=-\dfrac{1}{4} \dfrac{\sqrt{16-x^2}}{x}+C.$$
7. Find $\displaystyle\int \dfrac{1}{\sqrt{4+x^2}} \mathrm{d}x$.
Solution: Let $x=2\tan(\theta)$ so $\mathrm{d}x = 2\sec^2(\theta) \mathrm{d}\theta$ and
$$\dfrac{1}{\sqrt{4+x^2}} = \dfrac{1}{\sqrt{4+4\tan^2(\theta)}}=\dfrac{1}{2\sec(\theta)}.$$
Therefore compute
$$(*) \hspace{35pt} \begin{array}{ll}
\displaystyle\int \dfrac{1}{\sqrt{4+x^2}} \mathrm{d}x &= \dfrac{1}{2} \displaystyle\int \dfrac{1}{\tan(\theta)} 2\sec(\theta)\tan(\theta) \mathrm{d}\theta \\
&= \displaystyle\int \sec(\theta) \mathrm{d}\theta \\
&\stackrel{\mathrm{given}}{=} \ln(\tan(\theta)+\sec(\theta)) + C.
\end{array}$$
To finish, notice that our assignment $x=2\tan(\theta)$ tells us that $\dfrac{x}{2}=\tan(\theta)$, leading to the triangle
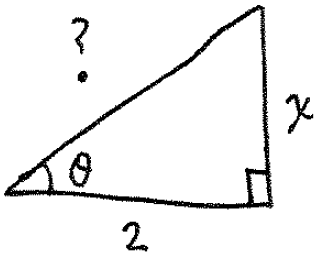
To find the missing side, use the Pythagorean theorem to write $2^2+x^2=?^2$, or $?=\sqrt{4+x^2}$. From this we observe that $\sec(\theta)=\dfrac{?}{2}=\dfrac{\sqrt{4+x^2}}{2}$. Finally, from $(*)$ we see
$$\begin{array}{ll}
\displaystyle\int \dfrac{1}{\sqrt{4+x^2}} \mathrm{d}x &= \ln(\tan(\theta)+\sec(\theta)) + C \\
&= \ln \left( \dfrac{x}{2} + \dfrac{\sqrt{4+x^2}}{2} \right) + C.
\end{array}$$
8. Find $\displaystyle\int x\sqrt{x^2-36} \mathrm{d}x$.
Solution: Let $x=6\sec(\theta)$ so that $\mathrm{d}x=6\sec(\theta)\tan(\theta) \mathrm{d}\theta$ and
$$x\sqrt{x^2-36} = 6\sec(\theta)\sqrt{36\sec^2(\theta)-36} = 36\sec(\theta)\tan(\theta).$$
Therefore we see
$$(*) \hspace{35pt} \begin{array}{ll}
\displaystyle\int x\sqrt{x^2-36} \mathrm{d}x &= 216 \displaystyle\int \sec^2(\theta)\tan^2(\theta) \mathrm{d}\theta \\
&\stackrel{u=\tan(\theta)}{=} 216 \displaystyle\int u^2 \mathrm{d}u \\
&= 216 \dfrac{u^3}{3} + C \\
&= \dfrac{216}{3} \tan^3(\theta)+C.
\end{array}$$
To finish, notice that our assignment $x=6\sec(\theta)$ shows that $\sec(\theta)=\dfrac{x}{6}$ yielding the following triangle:
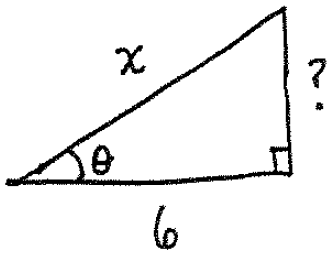
To find the missing side, use Pythagorean theorem to write $6^2+?^2=x^2$, or $?=\sqrt{x^2-36}$. Finally, from $(*)$ we see
$$\begin{array}{ll}
\displaystyle\int x\sqrt{x^2-36} \mathrm{d}x &= \dfrac{216}{3} \tan^3(\theta) + C \\
&= \dfrac{216}{3} \left( \dfrac{\sqrt{x^2-36}}{6} \right)^3 + C \\
&= \dfrac{\left( \sqrt{x^2-36} \right)^3}{3} + C.
\end{array}$$
9. Find $\displaystyle\int \dfrac{\sqrt{x^2-25}}{x} \mathrm{d}x$.
Solution: Let $x=5\sec(\theta)$ so $\mathrm{d}x=5\sec(\theta)\tan(\theta) \mathrm{d}\theta$ and
$$\dfrac{\sqrt{x^2-25}}{x}=\dfrac{\sqrt{25\sec^2(\theta)-25}}{5\sec(\theta)} = \dfrac{\tan(\theta)}{\sec(\theta)}.$$
Therefore compute
$$(*) \hspace{35pt} \begin{array}{ll}
\displaystyle\int \dfrac{\sqrt{x^2-25}}{x} \mathrm{d}x &= 5\displaystyle\int \dfrac{\tan(\theta)}{\sec(\theta)} \sec(\theta)\tan(\theta) \mathrm{d}\theta \\
&=5 \displaystyle\int \tan^2(\theta) \mathrm{d}\theta \\
&= 5 \displaystyle\int \sec^2(\theta)-1 \mathrm{d}\theta \\
&= 5 \tan(\theta) - 5\theta + C.
\end{array}$$
From our assignment $x=5\sec(\theta)$ we see that $\theta = \mathrm{arcsec} \left( \dfrac{x}{5} \right)$ and we can draw the following triangle:
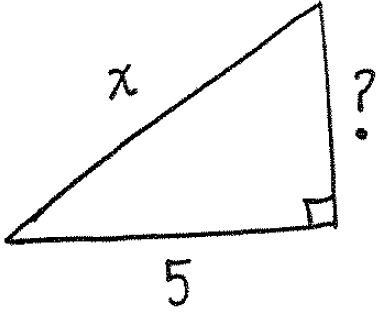
We find the missing side to be $?=\sqrt{x^2-25}$ and so $(*)$ tells us that
$$\begin{array}{ll}
\displaystyle\int \dfrac{\sqrt{x^2-25}}{x} \mathrm{d}x &= 5\tan(\theta)-5\theta + C \\
&= \sqrt{x^2-25} - 5\mathrm{arcsec} \left( \dfrac{x}{5} \right) + C.
\end{array}$$
Honors section
1. Use integration by parts to verify the following formula for an arbitrary $n>1$ (i.e. keep "$n$" in your integrals!):
$$\displaystyle\int \cos^n(x) \mathrm{d}x = \dfrac{\cos^{n-1}(x)\sin(x)}{n} + \dfrac{n-1}{n} \displaystyle\int \cos^{n-2}(x) \mathrm{d}x.$$
2. Use the formula from the previous problem to establish the following formulas:
a.) if $n$ is odd and $n \geq 3$, then
$$\displaystyle\int_0^{\frac{\pi}{2}} \cos^n(x) \mathrm{d}x = \left( \dfrac{2}{3} \right) \left( \dfrac{4}{5} \right) \left( \dfrac{6}{7} \right) \ldots \left( \dfrac{n-1}{n} \right).$$
b.) if $n$ is even and $n \geq 2$, then
$$\displaystyle\int_0^{\frac{\pi}{2}} \cos^n(x) \mathrm{d}x = \left( \dfrac{1}{2} \right) \left( \dfrac{3}{4} \right) \left( \dfrac{5}{6} \right) \ldots \left( \dfrac{n-1}{n} \right) \left( \dfrac{\pi}{2} \right).$$
3. Recall that an ellipse obeys the formula $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}=1$ for some $a,b > 0$.
a.) Solve this equation for $y$ to get an equation for the "top half" of the ellipse.
b.) Integrate the function from part a.) over the interval $[-a,a]$ and multiply by 2 to find a formula for the area of the ellipse.