Back to the class
Section 7.1 #25: Sketch the region bounded by $f(y)=y^2$ and $g(y)=y+2$ and find the area of the region.
Solution: First draw the described region:
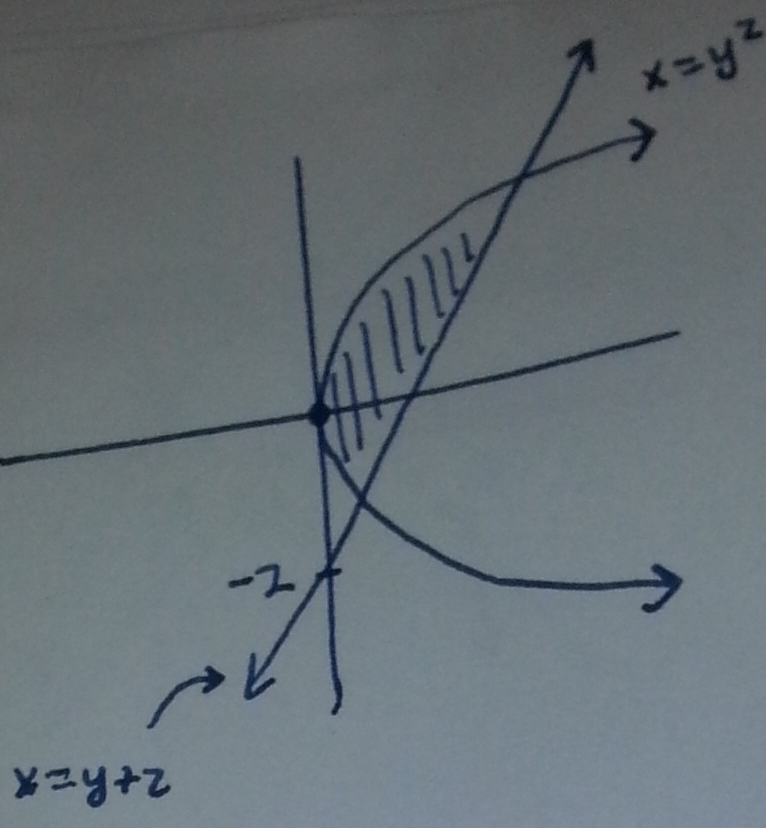
The intersection points can be found by setting $x=y^2$ and $x=y+2$ equal to each other to get the equation $y^2=y+2$, or more simply, $y^2-y-2=0$ which can be factored as $(y+1)(y-2)=0$ yielding $y=-1,2$. Therefore to find the area we compute
$$\begin{array}{ll}
\mathrm{Area} &= \displaystyle\int_{-1}^2 (y+2)-y^2 \mathrm{d}y \\
&= \dfrac{y^2}{2} + 2y - \dfrac{y^3}{3} \Bigg|_{-1}^2 \\
&= \left( \dfrac{4}{2} + 4 - \dfrac{8}{3} \right) - \left( \dfrac{1}{2} - 2 + \dfrac{1}{3} \right) \\
&= \dfrac{3}{2} + 6 -\dfrac{9}{3} \\
&= \dfrac{3}{2} + 3 \\
&= \dfrac{3}{2} + \dfrac{6}{2} \\
&= \dfrac{9}{2}.
\end{array}$$
Section 7.2 #17: Find the volume of the solid generated by revolving the region bounded by the graphs of $y=\dfrac{3}{1+x}$, $y=0$, $x=0$, and $x=3$ about the line $y=4$.
Solution: First draw the region:
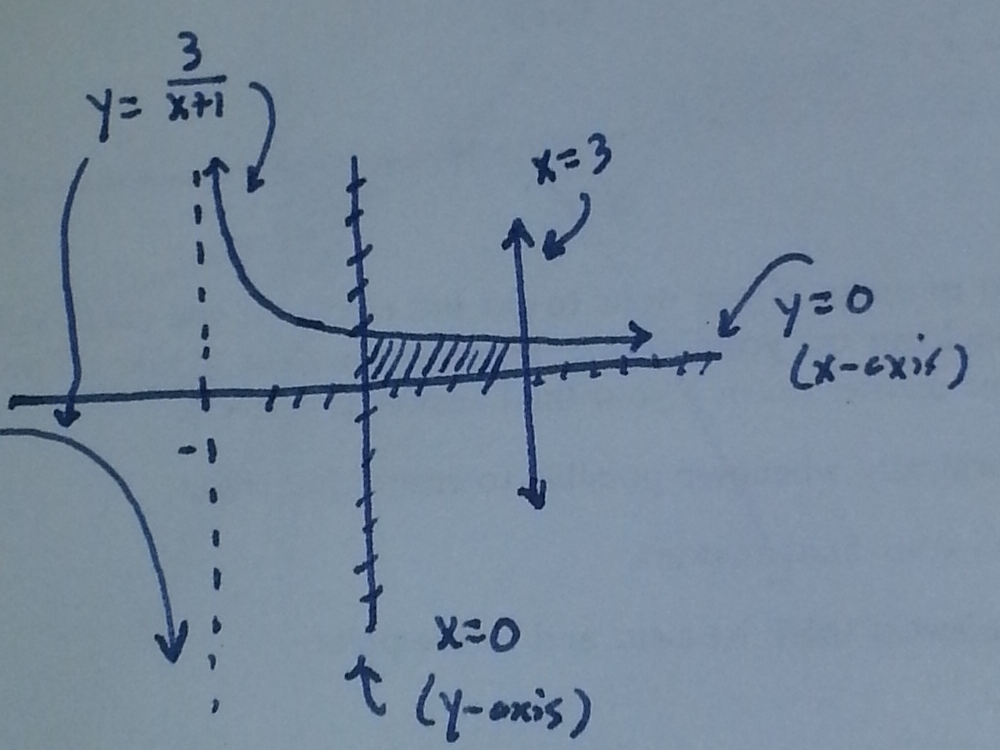
and now draw the washer:
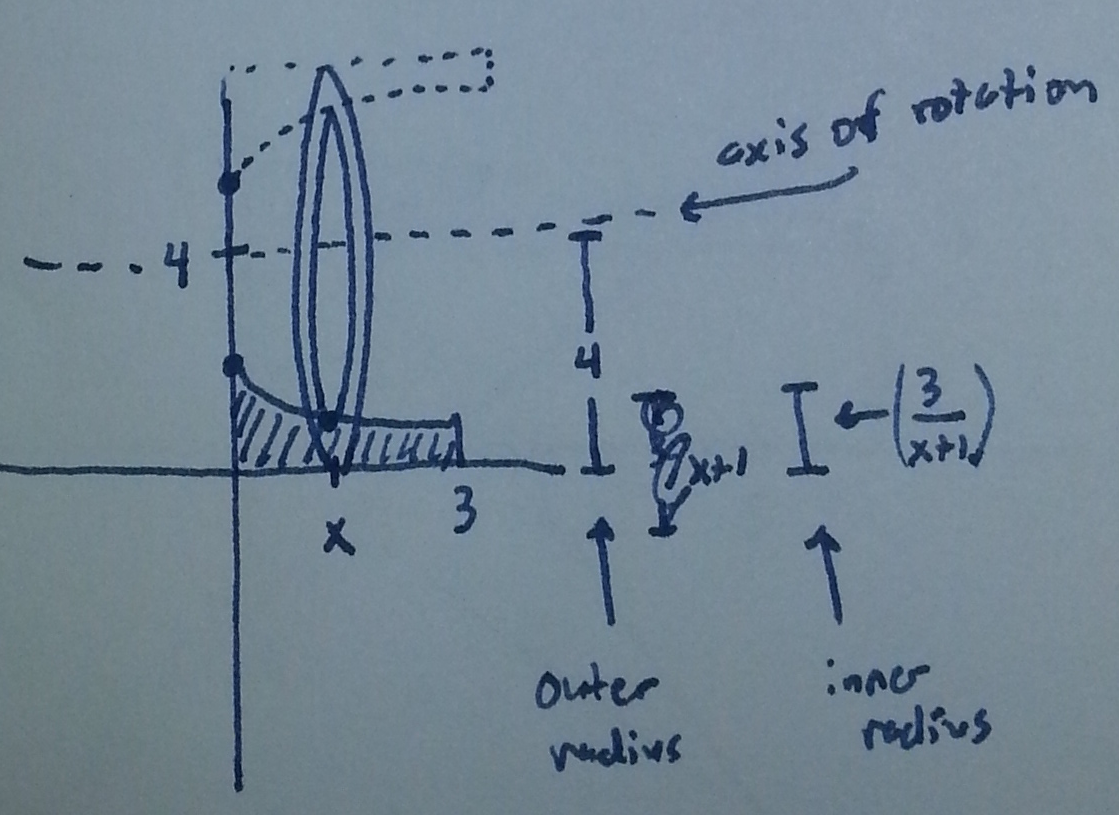
From this we compute
$$\begin{array}{ll}
\mathrm{Volume} &= \pi \displaystyle\int_0^3 4^2 - \left( 4 - \dfrac{3}{1+x} \right)^2 \mathrm{d}x \\
&=\pi \displaystyle\int_0^3 16 - \left( 16 - \dfrac{24}{x+1} + \dfrac{9}{(x+1)^2} \right) \mathrm{d}x \\
&= 24\pi \displaystyle\int_0^3 \dfrac{1}{x+1} \mathrm{d}x - 9\pi \displaystyle\int_0^3 \dfrac{1}{(x+1)^2} \mathrm{d}x \\
&\stackrel{u=x+1}{=} 24 \pi \displaystyle\int_1^4 \dfrac{1}{u} \mathrm{d}u - 9\pi \displaystyle\int_1^4 u^{-2} \mathrm{d}u \\
&=24\pi [\ln(4)-\ln(1)] - 9\pi \left[ -\dfrac{1}{u} \right|_1^4 \\
&=24\pi \ln(4) - 9\pi \left( -\dfrac{1}{4} - (-1) \right) \\
&\stackrel{\ln(2^2)=2\ln(2)}{=}48\pi \ln(2) - \dfrac{27\pi}{4}.
\end{array}$$
Section 7.2 #21: Find the volume of the solid generated by revolving the region bounded by the graphs of $x=y^2$ and $x=4$ about the line $x=5$.
Solution: Draw the described region:
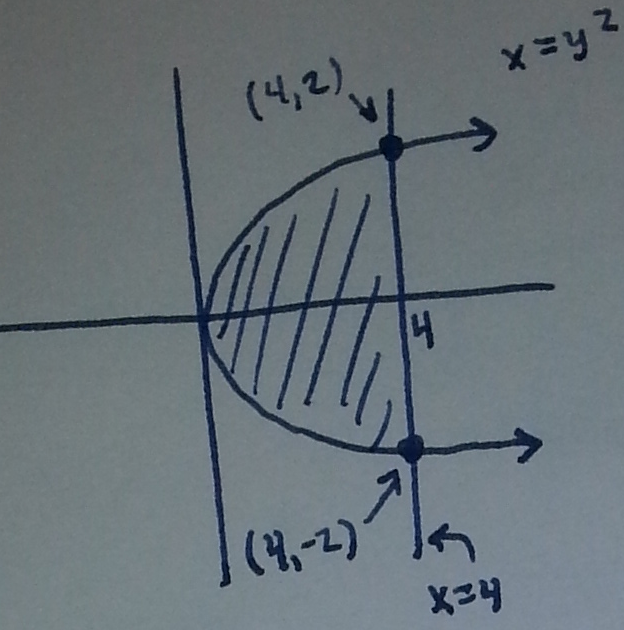
and the washer:
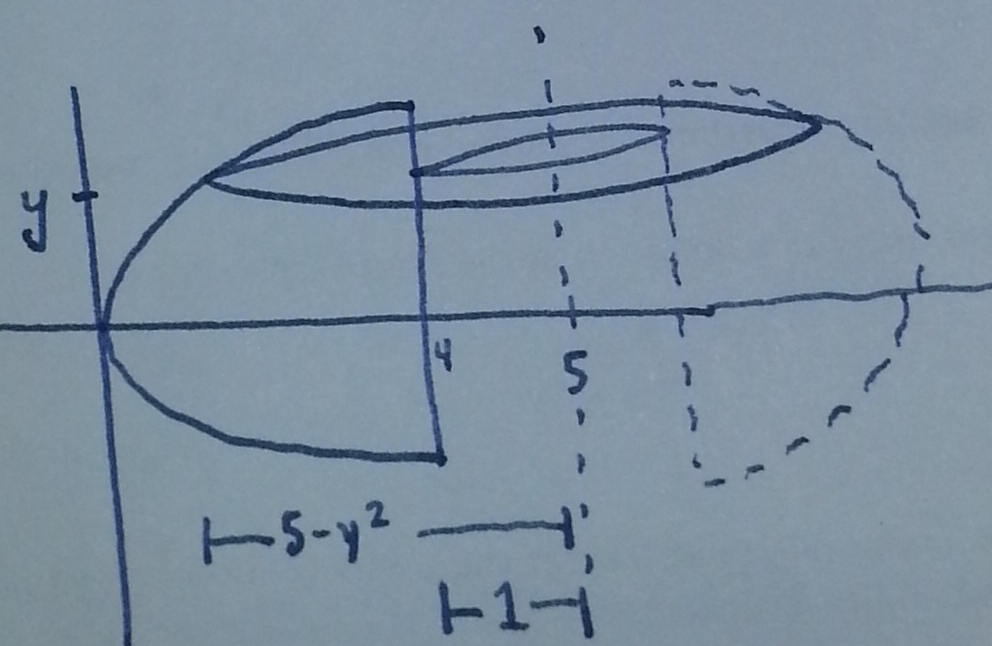
From this compute
$$\begin{array}{ll}
\mathrm{Volume} &= \pi \displaystyle\int_{-2}^2 (5-y^2)^2 - 1^2 \mathrm{d}y \\
&=\pi \displaystyle\int_{-2}^2 25 - 10y^2 + y^4 -1 \mathrm{d}y \\
&= \pi \displaystyle\int_{-2}^2 24 - 10y^2 + y^4 \mathrm{d}y \\
&= \pi \left[24y - \dfrac{10}{3} y^3 + \dfrac{1}{5}y^5 \right]_{-2}^2 \\
&= \pi \left[ \left( 48 - \dfrac{80}{3}+\dfrac{32}{5} \right) - \left( -48 + \dfrac{80}{3} -\dfrac{32}{5}\right) \right]\\
&= \pi \left[ 96 - \dfrac{160}{3} + \dfrac{64}{5} \right] \\
&= \dfrac{832\pi}{15}.
\end{array}$$
Section 7.3 #9: Set up and evaluate the integral that gives the volume of the solid generated by revolving the region bounded by $y=4x-x^2$, $x=0$, and $y=4$ about the line $x=5$. (NOTE: the given problem in the book said to rotate about the $y$-axis, which leads you to have to solve $4x-x^2=y$ for $x$...this essentially requires "completing the square" which I am not testing you on right now, so I will leave this "incorrect" version of the problem since it illustrates things nicely.)
Solution: First draw the region:
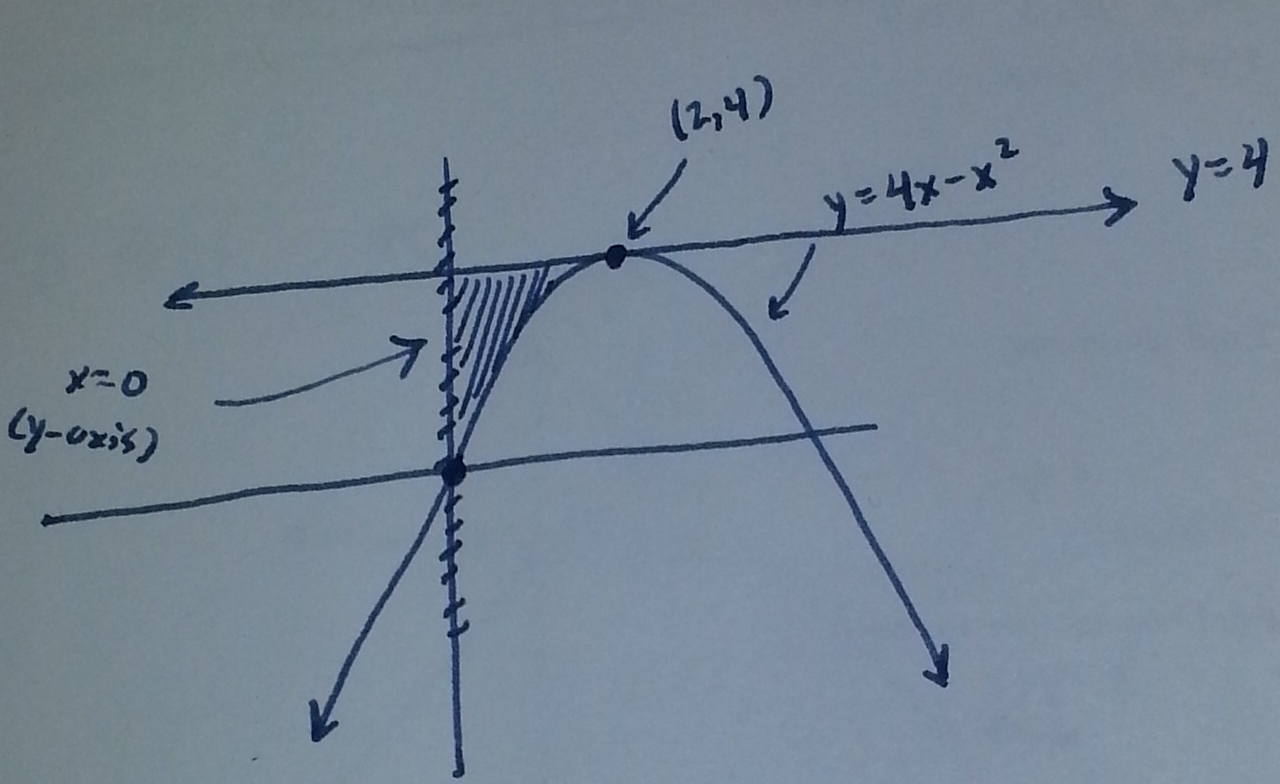
and draw the cylindrical shell
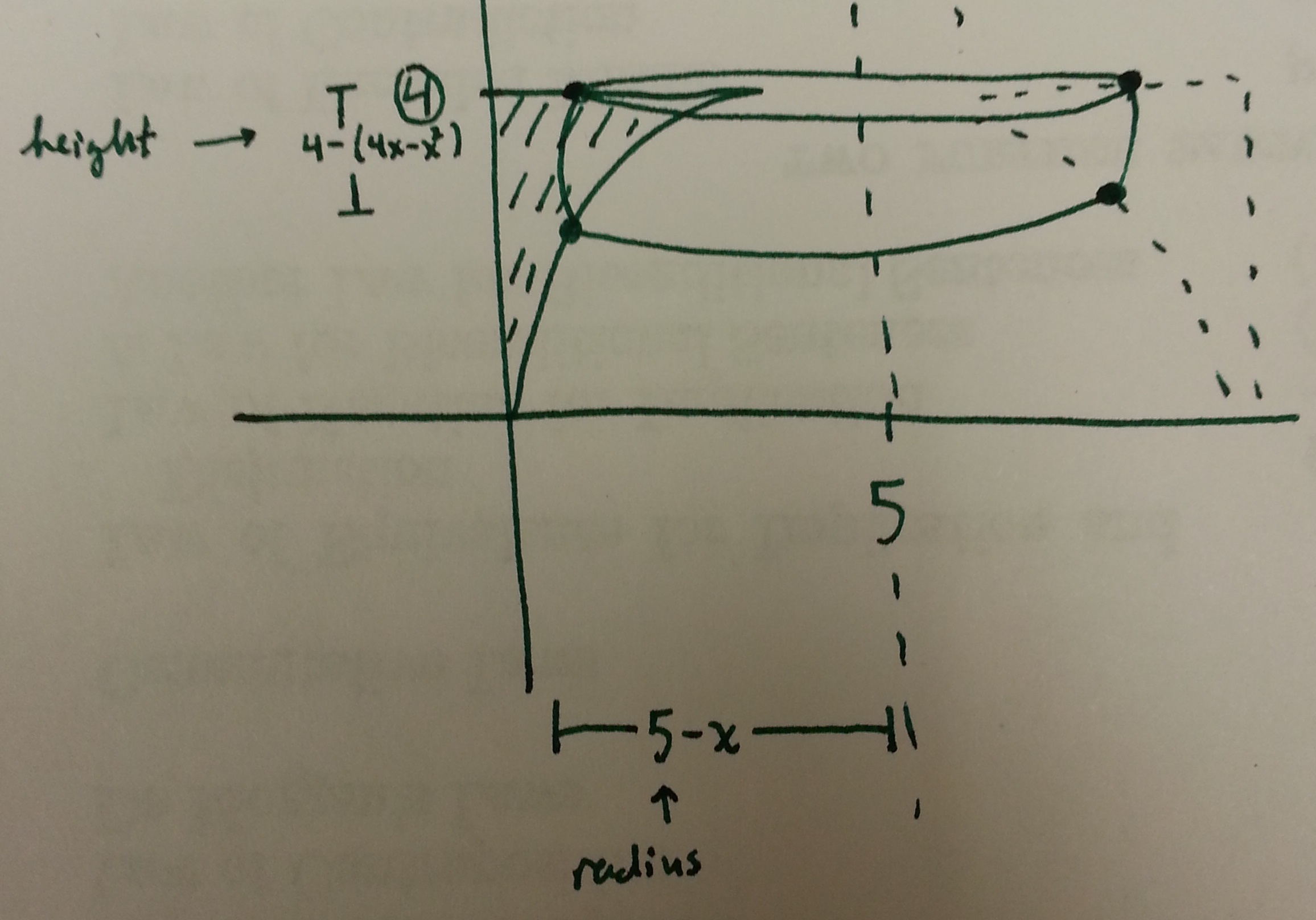
Now compute
$$\begin{array}{ll}
\mathrm{Volume} &= 2\pi \displaystyle\int_0^2 (4-(4x-x^2))(5-x) \mathrm{d}x \\
&= 2\pi \displaystyle\int_0^2 (x^2-4x+4)(5-x) \mathrm{d}x \\
&=2\pi \displaystyle\int_0^2 -x^3+9x^2-24x+20 \mathrm{d}x \\
&=2\pi \left[ -\dfrac{x^4}{4} + 3x^3 - 12x^2+20x \right|_0^2 \\
&=2\pi \left[ \left( -\dfrac{2^4}{4} + 3(2)^3-12(2^2)+20(2)\right) - \left(0 \right) \right] \\
&= 2\pi \left( -4+24-48+40 \right) \\
&=24\pi.
\end{array}$$
Section 7.3 #21: Use the shell method to set up and evaluate the integral that gives the volume of the solid generaated by revolving the plane region bounded by $x+y=4$, $y=x$, and $y=0$ about the $x$-axis.
Solution: First draw the region:
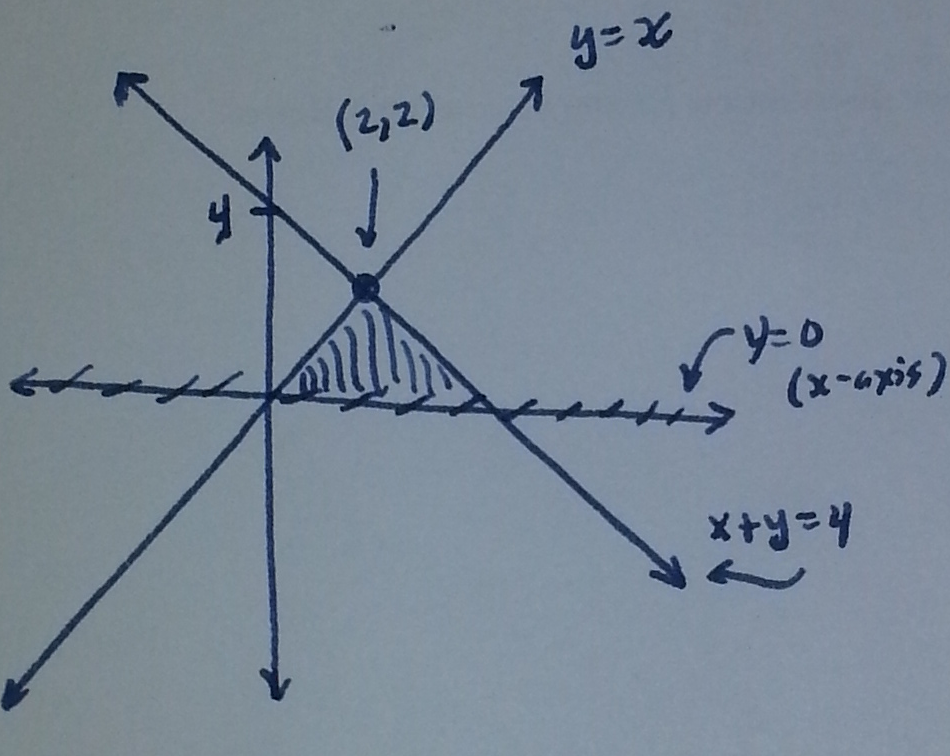
and draw the cylindrical shell
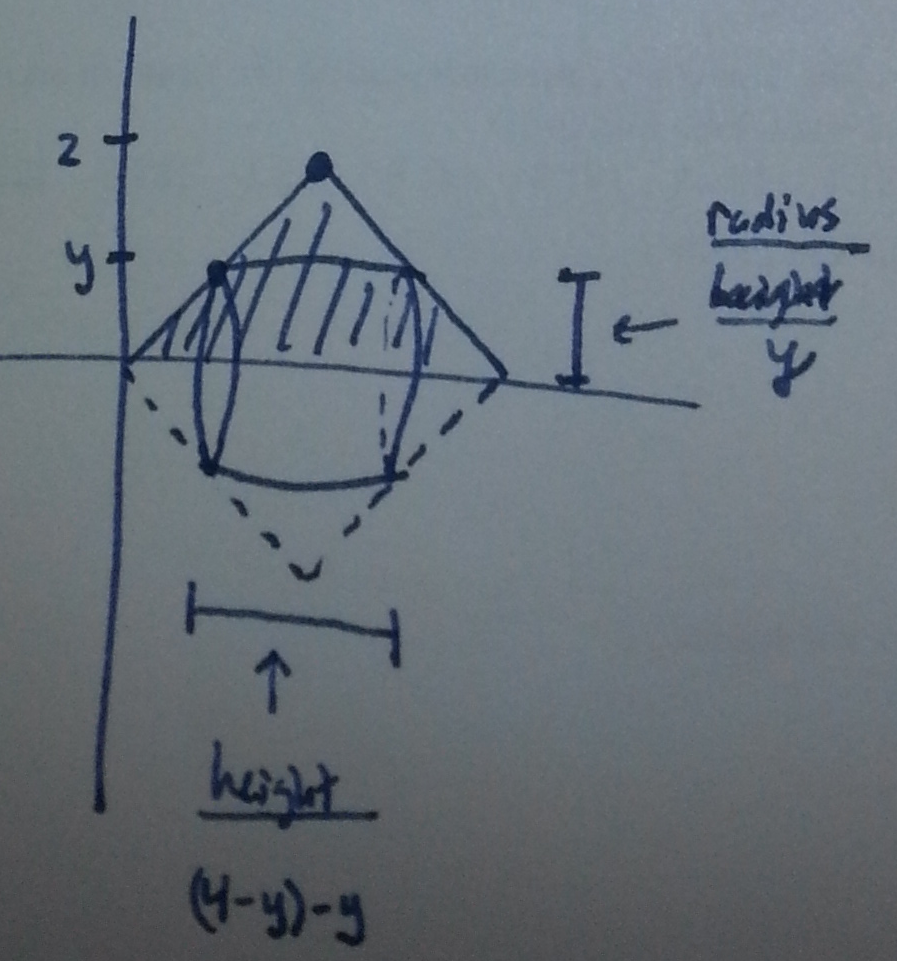
To find the volume, compute
$$\begin{array}{ll}
\mathrm{Volume} &= 2\pi \displaystyle\int_0^2 y((4-y)-y) \mathrm{d}y \\
&= 2\pi \displaystyle\int_0^2 4y-2y^2 \mathrm{d}y \\
&= 2\pi \left[ 2y^2 - \dfrac{2}{3} y^3 \right|_0^2 \\
&=2 \pi \left[ \left( 8 - \dfrac{16}{3} \right) - 0 \right] \\
&=\dfrac{16\pi}{3}.
\end{array}$$











