Back to the class
Section 7.1 #5: Set up the integral that gives the area of the region: where $y_1(x)=3(x^3-x)$ and $y_2(x)=0$.
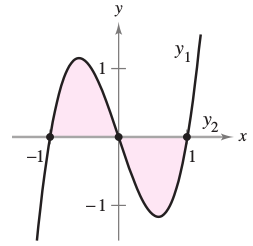
Solution: The pictured area requires two integrals:
$$\mathrm{area} = \displaystyle\int_{-1}^0 3(x^3-x) - 0 \mathrm{d}x + \displaystyle\int_0^1 0 - 3(x^3-x) \mathrm{d}x=-6\displaystyle\int_0^1 -x+x^3 \mathrm{d}x. $$
Section 7.1 #16: Find the area of the region
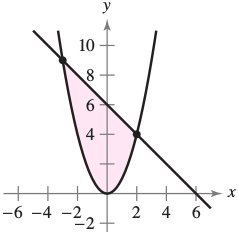 ,
,
where the curves $y=x^2$ and $y=6-x$ are pictured by integrating
a.) with respect to $x$, and
b.) with respect to $y$.
Solution: For part a.), the "top curve" is $y=6-x$ and the "bottom curve" is $y=x^2$. The $x$-values of the intersection points are $x=-3$ and $x=2$, so compute
$$\begin{array}{ll}
\displaystyle\int_{-3}^2 (6-x)-x^2 \mathrm{d}x &= 6x - \dfrac{x^2}{2} - \dfrac{x^3}{3} \Bigg|_{-3}^2 \\
&= \left( 12 - \dfrac{4}{2} - \dfrac{8}{3} \right) - \left( -18 - \dfrac{9}{2} + \dfrac{27}{3} \right) \\
&=30+\dfrac{5}{2}-\dfrac{35}{3} \\
&=\dfrac{180}{6} + \dfrac{15}{6} - \dfrac{70}{6} \\
&=\dfrac{125}{6}.
\end{array}$$
For part b.), first solve $y=x^2$ for $x$ to get $x=\pm \sqrt{y}$ and then solve $y=6-x$ for $x$ to get $x=6-y$. The "right curve" depends on the height -- between $y=0$ and $y=4$ the "right curve" is $x=\sqrt{y}$ and between $y=4$ and $y=9$ the "right curve" is $x=6-y$. The left curve is always $x=-\sqrt{y}$. This means we need two integrals as follows: compute
$$\begin{array}
\displaystyle\int_0^4 \sqrt{y} - (-\sqrt{y}) \mathrm{d}y + \displaystyle\int_4^9 (6-y)-(-\sqrt{y}) \mathrm{d}y &= 2 \displaystyle\int_0^4 y^{\frac{1}{2}} \mathrm{d}y + \displaystyle\int_4^9 6-y+y^{\frac{1}{2}} \mathrm{d}y \\
&= \dfrac{4}{3}y^{\frac{3}{2}} \Bigg|_0^4 + \left[ 6y - \dfrac{y^2}{2} + \dfrac{2}{3}y^{\frac{3}{2}} \right|_4^9 \\
&= \left( \dfrac{4}{3} \right) 4^{\frac{3}{2}} + \left[ \left( 54 - \dfrac{81}{2} + \dfrac{2}{3} 9^{\frac{3}{2}} \right) - \left( 24-\dfrac{16}{2}+\dfrac{2}{3}4^{\frac{3}{2}} \right) \right] \\
&= \dfrac{125}{6}.
\end{array}$$
Section 7.1 #23: Sketch the region bounded by the graphs of the equations $f(x)=\sqrt{x}+3$ and $g(x)=\dfrac{1}{2}x + 3$ and find the area of the region.
Solution: Sketch:
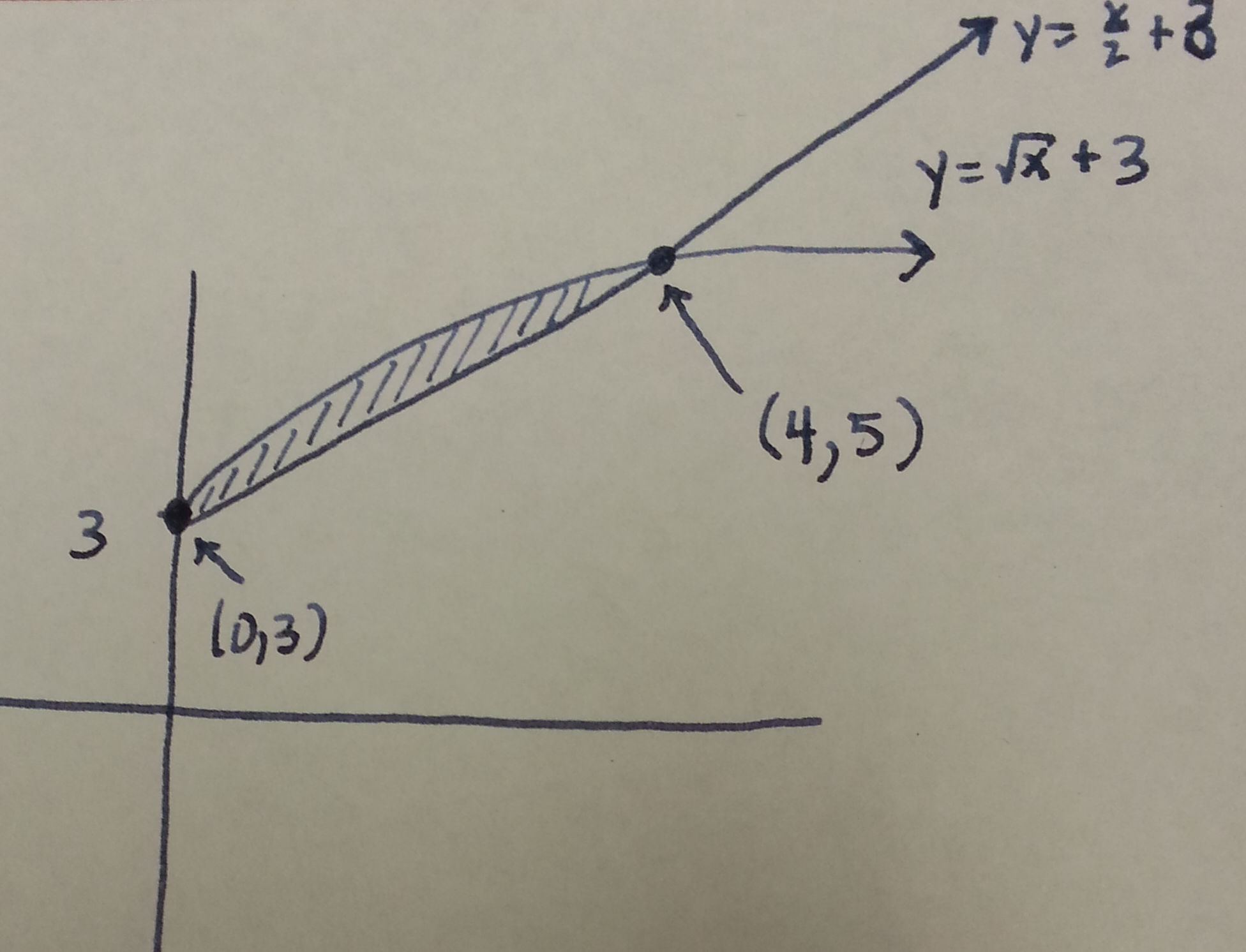
Compute
$$\begin{array}{ll}
\displaystyle\int_0^4 (\sqrt{x}+3) - \left( \dfrac{1}{2} x + 3 \right) \mathrm{d}x &= \displaystyle\int_0^4 x^{\frac{1}{2}} - \dfrac{1}{2} x \mathrm{d}x \\
&= \dfrac{2}{3} x^{\frac{3}{2}} - \dfrac{1}{4} x^2 \Bigg|_0^4 \\
&= \left( \dfrac{2}{3} 4^{\frac{3}{2}} - \dfrac{1}{4} 4^2 \right) - 0\\
&= \dfrac{16}{3} - 4 \\
&= \dfrac{16}{3} - \frac{12}{3} \\
&= \dfrac{4}{3}.
\end{array}$$
Section 10.1 #1-6: a, e, c, b, f, d




 ,
,