Back to the class
Section 10.1 #1-6: a, e, c, b, f, d
Section 10.2 #13: Sketch the curve represented by the parametric equation and write the corresponding rectangular equation by eliminating the parameter:
$$\left\{ \begin{array}{ll}
x(t) &= e^t \\
y(t) &= e^{3t}+1.
\end{array} \right.$$
Solution: First sketch the curve:
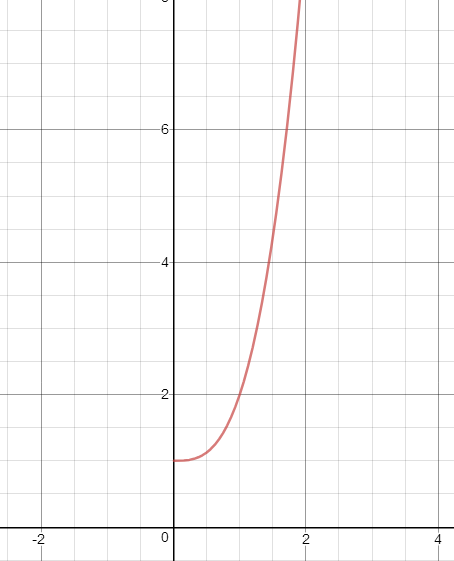To eliminate the parameter, solve for $t$ in the equations defining $x(t)$ and $y(t)$, first
$$\log(x)=t,$$
and second
$$\log(y-1)=3t,$$
and hence
$$\dfrac{1}{3}\log(y-1)=t.$$
Now set these expressions equal:
$$\dfrac{1}{3} \log(y-1)=t=\log(x),$$
or in other words,
$$\log(y-1)=3\log(x),$$
so
$$\log(y-1)=\log(x^3).$$
Now take $\exp$ of both sides to get
$$y-1 = x^3,$$
or in other words,
$$y=x^3+1.$$
Section 10.3 #21: Find an equation for the tangent line to the parametric equations $\left\{ \begin{array}{ll}
x(t) = t^2-t \\
y(t)=t^3-3t
\end{array} \right.$ at parameter value $t=-1$.
Solution: Consider the curve in question:
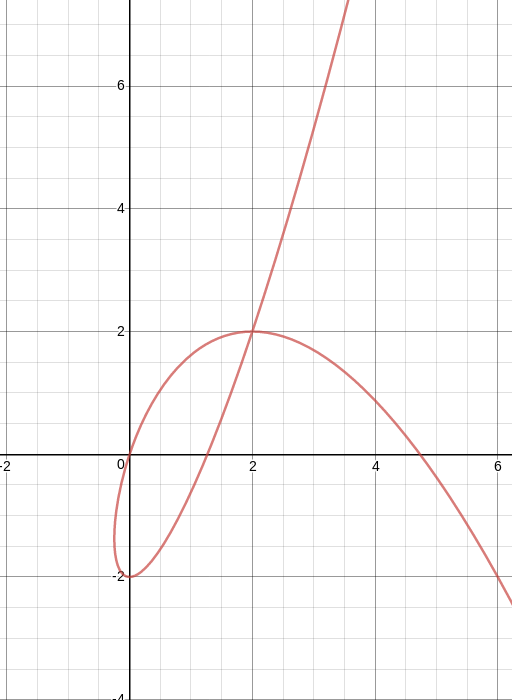Note that the point in question correpsonding to the parameter value $t=-1$ can be found by plugging that $t$ into $x$ and $y$ to get $(0,2)$. Now find $\dfrac{\mathrm{d}y}{\mathrm{d}x}$:
$$\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{y'(t)}{x'(t)}=\dfrac{3t^2-3}{2t-1}.$$
Therefore the slope of the curve corresponding to the parameter value $t=-1$ is
$$\dfrac{\mathrm{d}y}{\mathrm{d}x}\Bigg|_{t=-1} = \dfrac{3(-1)^2-3}{2(-1)-1} = \dfrac{0}{-3} = 0.$$
Hence the equation of the tangent line is the equation of the line with slope $0$ passing through the point $(0,2)$, i.e. it obeys the equation
$$y-2=0,$$
or
$$y=2,$$
as pictured:
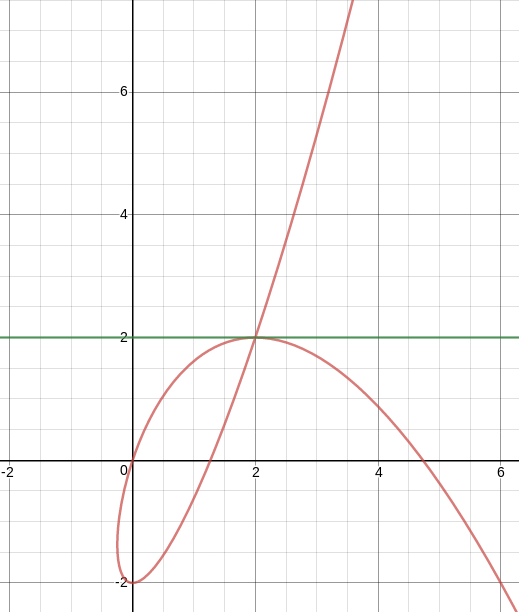
Section 10.4 #2: Plot the point in polar coordinates and find the correspoding rectangular coordinates for the point: $(r,\theta)=\left( -2, \dfrac{5\pi}{3} \right)$.
Solution: First plot the point:
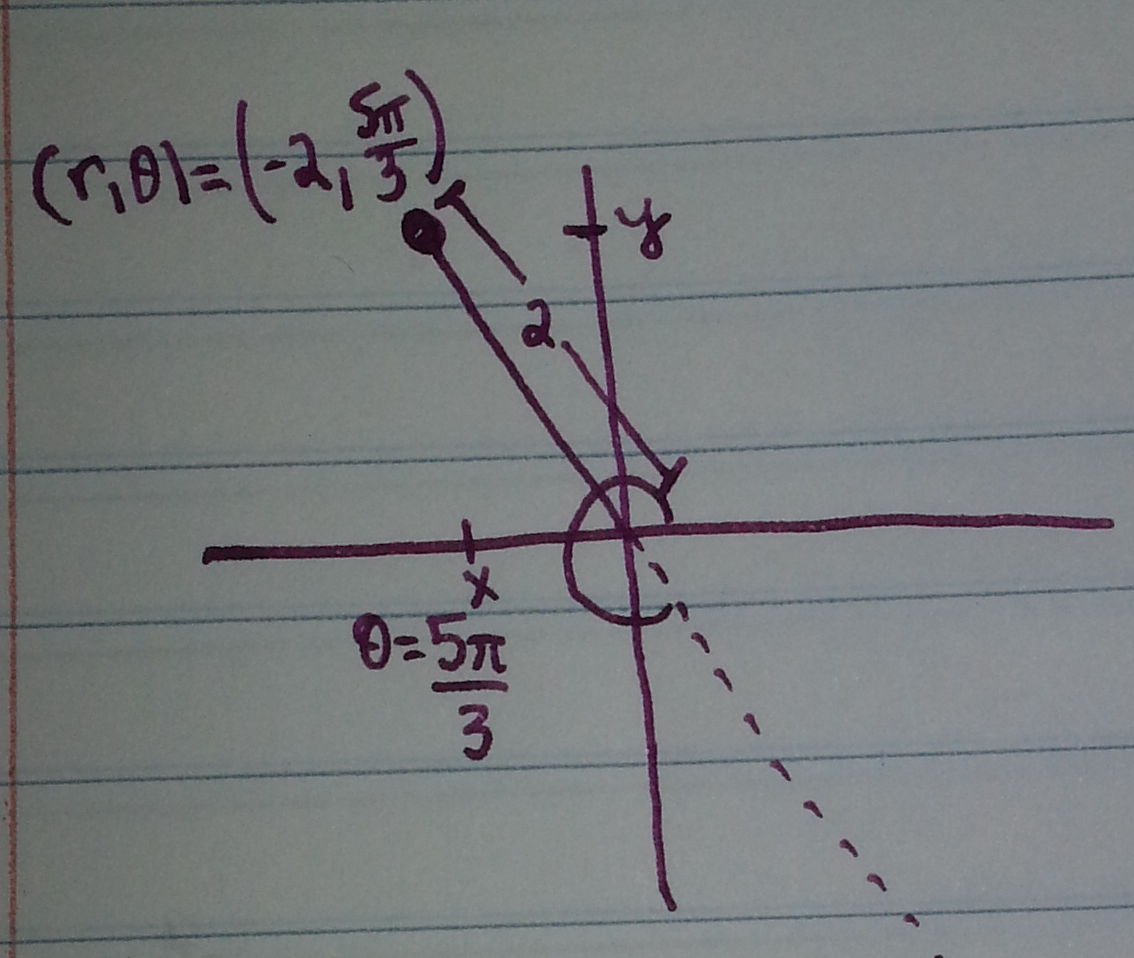To find the rectangular coordinates, we exploit the formula
$$\left\{ \begin{array}{ll}
x=r\cos(\theta) \\
y=r\sin(\theta)
\end{array}\right.$$
to see that
$$\left\{ \begin{array}{ll}
x= -2 \cos \left( \dfrac{5\pi}{3} \right) = (-2) \left( \dfrac{1}{2} \right) = -1 \\
y= -2 \sin \left( \dfrac{5\pi}{3} \right) = (-2) \left( -\dfrac{\sqrt{3}}{2} \right) = \sqrt{3}.
\end{array} \right.$$
Therefore the rectangular coordinates of the point are $(-1,\sqrt{3})$.
Section 10.4 #16: Plot the point and find polar coordinates for it: $(3,-\sqrt{3})$.
Solution: First plot the point:
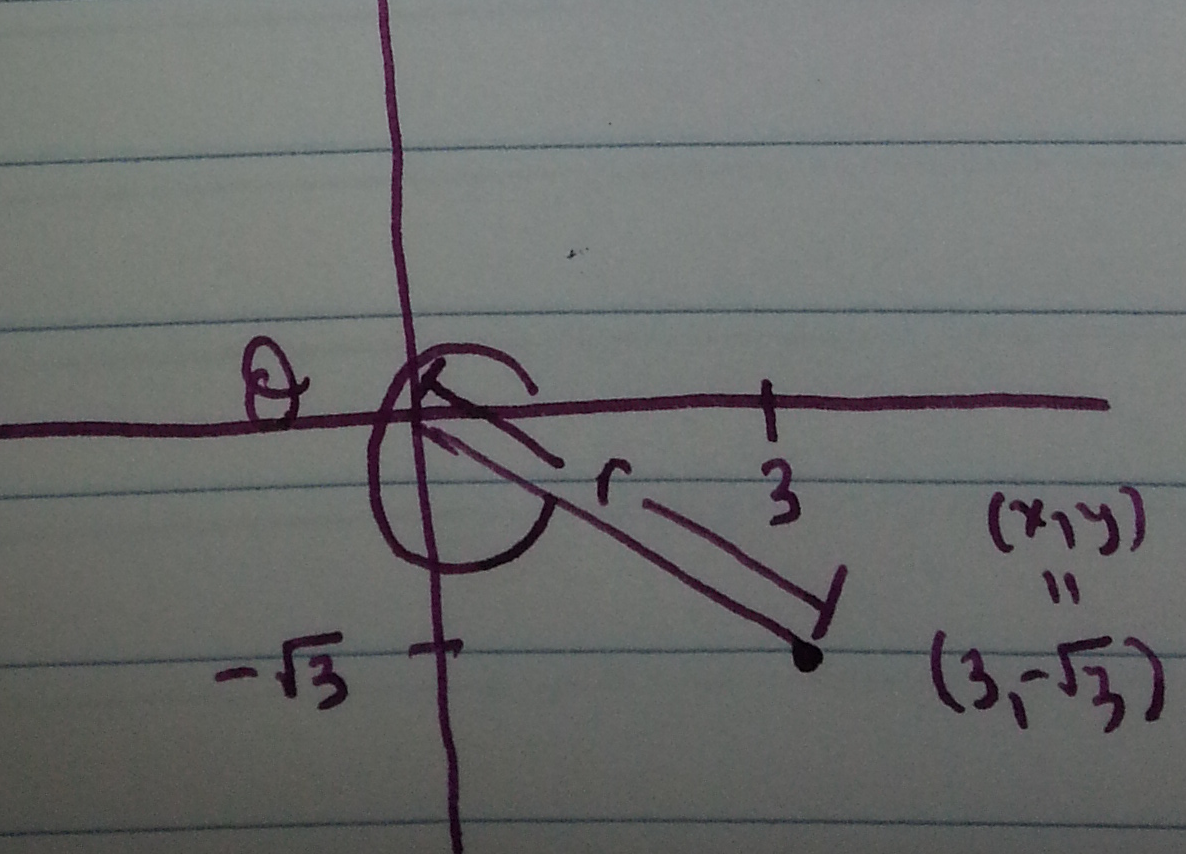To find the polar coordinates, we use the formulas
$$\left\{ \begin{array}{ll}
r=\sqrt{x^2+y^2} \\
\theta = \left\{ \begin{array}{ll}
\arctan \left( \dfrac{y}{x} \right) & (x,y) \mathrm{\hspace{2pt} is \hspace{2pt} quadrants \hspace{2pt} I \hspace{2pt} or \hspace{2pt} II} \\
\pi+\arctan \left( \dfrac{y}{x} \right) & (x,y) \mathrm{\hspace{2pt} is \hspace{2pt} quadrants \hspace{2pt} III \hspace{2pt} or \hspace{2pt} IV}
\end{array} \right.
\end{array} \right.$$
So compute
$$\left\{ \begin{array}{ll}
r = \sqrt{3^2 + (-\sqrt{3})^2} = \sqrt{9+3} = \sqrt{12} \\
\theta \stackrel{\mathrm{QIV}}{=} \arctan \left( \dfrac{-\sqrt{3}}{3} \right) = -\dfrac{\pi}{6}.
\end{array} \right.$$
Therefore the polar coordinates of the point are $(r,\theta)=\left(\sqrt{12}, -\dfrac{\pi}{6} \right)$.
