Back to the class
In Honors HW3, you found a scheme to find solutions to the equation $\Delta y(x)=y(x)$ once an "initial value" was given by turning it into $y(x+1)=2y(x)$. Let us program this into a spreadsheet program (i.e. Microsoft Office, OpenOffice Calc, or Google Sheets). Open your favorite spreadsheet program and make a column for the variable "$x$" and list the first few non-negative integers:
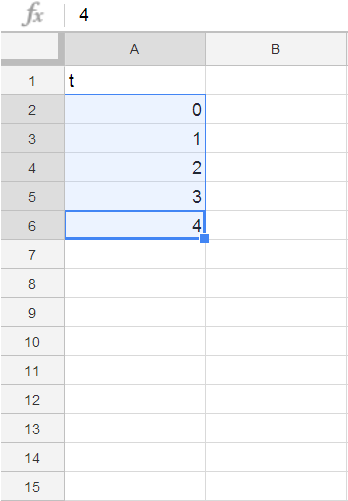 Highlight your first few non-negative integers and drag the little blue square in the bottom right down so that you get 50 values. In a far right column, place a number (say, $3$) to represent the "initial condition" $y(0)$ of our sequence:
Highlight your first few non-negative integers and drag the little blue square in the bottom right down so that you get 50 values. In a far right column, place a number (say, $3$) to represent the "initial condition" $y(0)$ of our sequence:
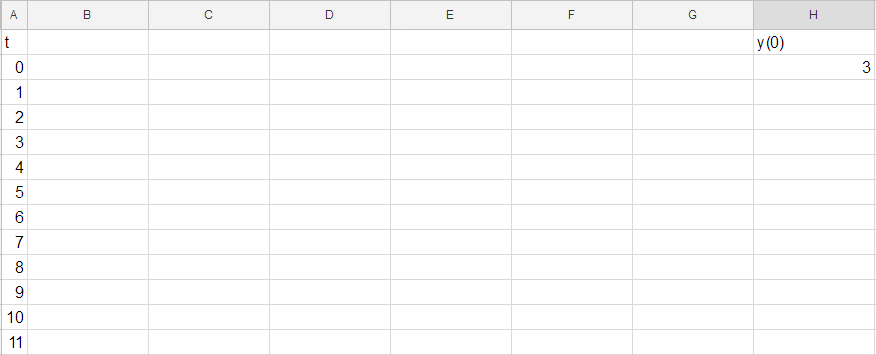 Now we must code in the recurrence. It was found in Honors HW3, Problem 2 that
$$y(x+1)=2y(x),$$
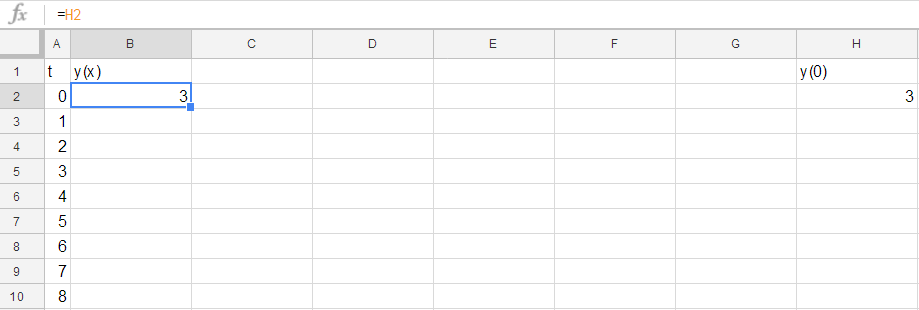
and so we must encode that in. To do this, first make a column to represent $y(x)$ (use the second column) and in the next row down put an "=" sign (meaning "there is a formula to come") and then click the cell which contains your numerical value. The effect will be to place the location of that cell into your new cell as such (note at the top it says "=H2", that's the kind of thing you're wanting here):
Now we must code in the recurrence. It was found in Honors HW3, Problem 2 that
$$y(x+1)=2y(x),$$
and so we must encode that in. To do this, first make a column to represent $y(x)$ (use the second column) and in the next row down put an "=" sign (meaning "there is a formula to come") and then click the cell which contains your numerical value. The effect will be to place the location of that cell into your new cell as such (note at the top it says "=H2", that's the kind of thing you're wanting here):
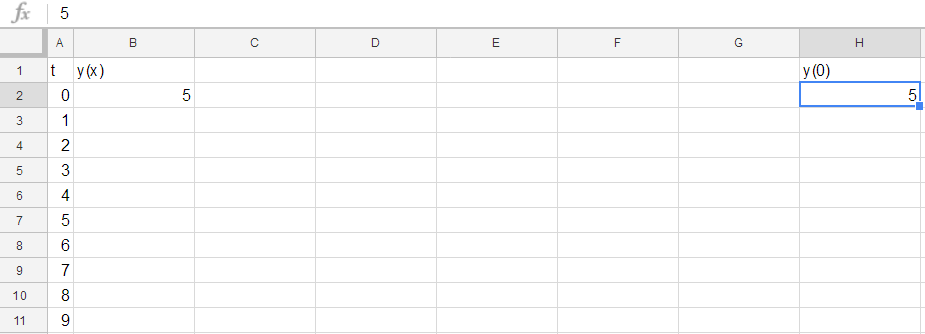
 Notice that if you change the value in the cell to the right, the value in the cell you just created will change appropriately:
Notice that if you change the value in the cell to the right, the value in the cell you just created will change appropriately:
 Now we must code in the "recurrence relation" $y(x+1)=2y(x)$. To do it, in the cell below the one you most recently created, we want to put an "=" sign and then type "2*" and then click the cell immediately above the one you are writing in. The effect should be to give you a formula like the following:
Now we must code in the "recurrence relation" $y(x+1)=2y(x)$. To do it, in the cell below the one you most recently created, we want to put an "=" sign and then type "2*" and then click the cell immediately above the one you are writing in. The effect should be to give you a formula like the following:
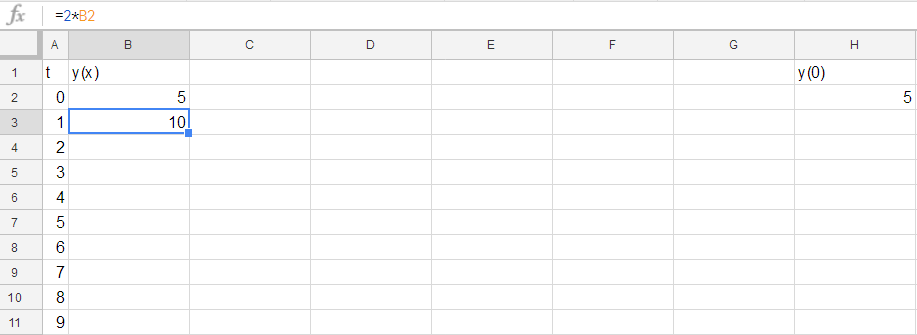 Now all you must do is highlight the cell you just created and drag the square in the bottom right down and it will extend your formula downwards, replacing (in my image) "B2" with "B3" in the cell below, "B4" below that, etc:
Now all you must do is highlight the cell you just created and drag the square in the bottom right down and it will extend your formula downwards, replacing (in my image) "B2" with "B3" in the cell below, "B4" below that, etc:
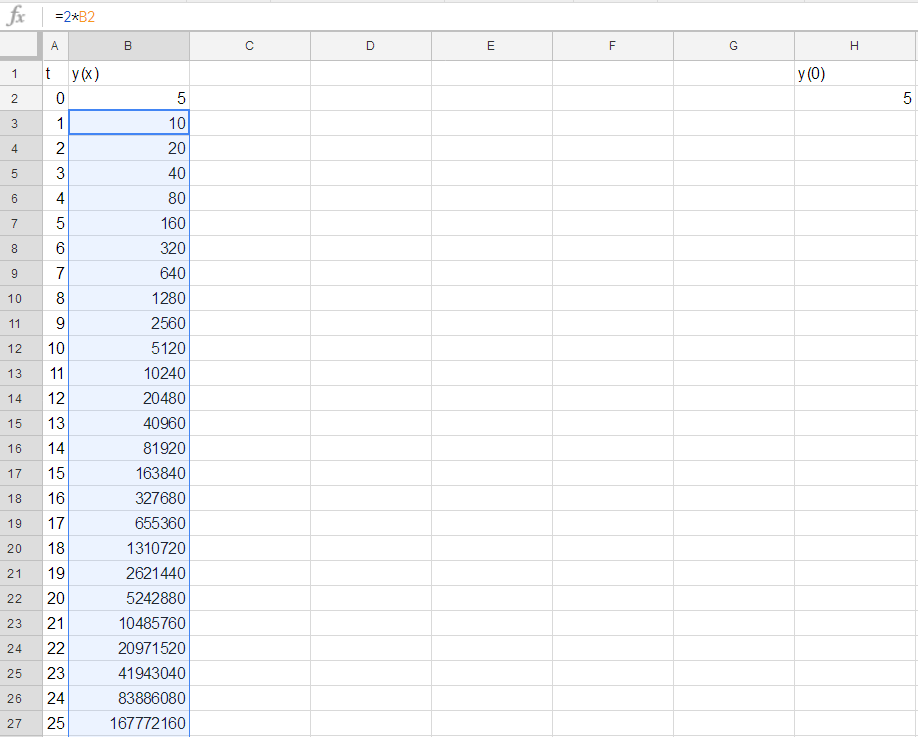 Notice that now changing the initial condition propagates into your new values:
Notice that now changing the initial condition propagates into your new values:
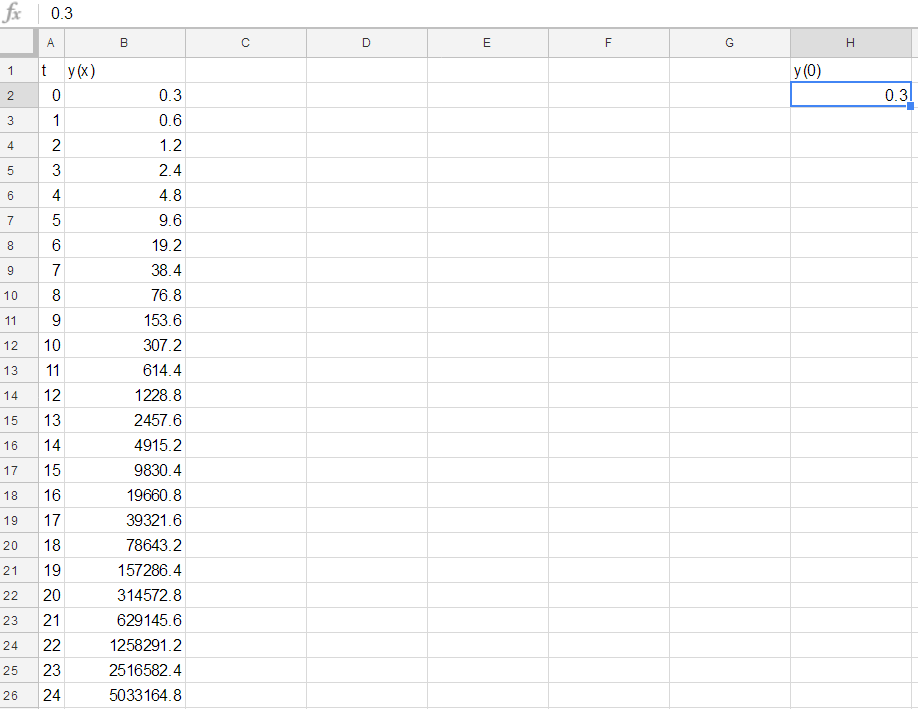 Notice that the answers from Honors Homework 3 can be found in this spreadsheet with appropriate initial values (for example, set the initial condition to be $1$ to recover the solutions for Honors HW 3 Problem 3).
Consider the following equation with an unknown function $y(x)$:
$$\Delta y(x)=\dfrac{y(x)}{x+1}.$$
1. Expand the left-hand side of this equation using the definition of $\Delta$ (from Honors HW1).
Notice that the answers from Honors Homework 3 can be found in this spreadsheet with appropriate initial values (for example, set the initial condition to be $1$ to recover the solutions for Honors HW 3 Problem 3).
Consider the following equation with an unknown function $y(x)$:
$$\Delta y(x)=\dfrac{y(x)}{x+1}.$$
1. Expand the left-hand side of this equation using the definition of $\Delta$ (from Honors HW1).
2. Solve the resulting equation from Problem 1 for $y(x)$.
3. Create a spreadsheet program to find the solutions, depending on an initial value $y(0)$. (e-mail me your spreadsheet to get graded on this problem)
4. If $y(0)=3$, then use your spreadsheet program to find $y(10)$, $y(30)$, and $y(50)$.
5. If $y(0)=0.5$, then use your spreadsheet program to find $y(10)$, $y(30)$, and $y(50)$.









