Back to the class
Section 9.1 #29: Prove the identity
$$\cos(x) - \cos^3(x) = \cos(x) \sin^2(x).$$
Solution: Recall the Pythagorean identity $\cos^2(x)+\sin^2(x)=1$ and rearrange it to say $\cos^2(x)=1-\sin^2(x)$. Start with the left and calculate
$$\begin{array}{ll}
\cos(x) - \cos^3(x) &= \cos(x)(1-\cos^2(x)) \\
&= \cos(x)\sin^2(x),
\end{array}$$
completing the proof. $\blacksquare$
Section 9.1 #30: Prove the identity
$$\cos(x)(\tan(x)-\sec(-x))=\sin(x)-1.$$
Solution: Recall the "even property" of cosine, i.e. $\cos(-x)=\cos(x)$. Start with the left and calculate
$$\begin{array}{ll}
\cos(x)(\tan(x)-\sec(-x))=\sin(x)-1 &= \cos(x) \left( \dfrac{\sin(x)}{\cos(x)} - \dfrac{1}{\cos(-x)} \right) = \sin(x)-1 \\
&= \cos(x) \left( \dfrac{\sin(x)}{\cos(x)} - \dfrac{1}{\cos(x)} \right) \\
&=\cos(x) \left( \dfrac{\sin(x)-1}{\cos(x)} \right) \\
&= \sin(x)-1,
\end{array}$$
completing the proof. $\blacksquare$
Section 9.1 #33: Prove the identtiy
$$\cos^2(x) - \tan^2(x) = 2-\sin^2(x)-\sec^2(x).$$
Solution: Recall from the Pythagorean identity $\cos^2(x)+\sin^2(x)=1$ we may conclude both $1-\sin^2(x)=\cos^2(x)$ and $\cos^2(x)-1=-\sin^2(x)$ . Start with the right and calculate
$$\begin{array}{ll}
2-\sin^2(x)-\sec^2(x) &= 2 - \sin^2(x) - \dfrac{1}{\cos^2(x)} \\
&= (1-\sin^2(x)) + 1 - \dfrac{1}{\cos^2(x)} \\
&= \cos^2(x) + \dfrac{\cos^2(x)-1}{\cos^2(x)} \\
&= \cos^2(x) + \dfrac{-\sin^2(x)}{\cos^2(x)} \\
&= \cos^2(x) - \tan^2(x),
\end{array}$$
completing the proof. $\blacksquare$
Section 9.1 #34: Prove or disprove whether or not the following equation is an identity:
$$\dfrac{1}{1+\cos(x)} - \dfrac{1}{1-\cos(-x)} = -2\cot(x)\csc(x).$$
Solution: Let us try a couple test values. First try $x=\dfrac{\pi}{6}$: calculate the left-hand side
$$\dfrac{1}{1+\cos(\frac{\pi}{6})} - \frac{1}{1-\cos(-\frac{\pi}{6})} = \dfrac{1}{1+\frac{\sqrt{3}}{2}} - \dfrac{1}{1-\frac{\sqrt{3}}{2}} = -4\sqrt{3},$$
now calculate the right-hand side
$$-2 \cot \left( \dfrac{\pi}{6} \right) \csc \left( \dfrac{\pi}{6} \right) = ... = -4\sqrt{3}.$$
They match. Now try a different value, say, $x=\dfrac{\pi}{3}$ (you will find that it works ok). So now try to prove it as an identity: start with the left and compute
$$\begin{array}{ll}
\dfrac{1}{1+\cos(x)} - \dfrac{1}{1-\cos(-x)} &= \dfrac{(1-\cos(-x))-(1+\cos(x))}{(1+\cos(x))(1-\cos(-x))} \\
&=\dfrac{-2\cos(x)}{1-\cos^2(x)} \\
&= \dfrac{-2\cos(x)}{\sin^2(x)} \\
&= -2 \left( \dfrac{\cos(x)}{\sin(x)} \right) \left( \dfrac{1}{\sin(x)} \right) \\
&= -2\cot(x)\csc(x),
\end{array}$$
completing the proof. $\blacksquare$
Section 9.1 #37: Prove or disprove whether the following equation is an identity:
$$\dfrac{\tan(x)}{\sec(x)} \sin(-x) = \cos^2(x).$$
Solution: Test a value for $x$, say $x=\dfrac{\pi}{4}$. Plugging this in for $x$ in the left-hand side yields
$$\dfrac{\tan(\frac{\pi}{4})}{\sec(\frac{\pi}{4})} \sin \left( - \dfrac{\pi}{4} \right) = \dfrac{1}{\frac{2}{\sqrt{2}}} \left( - \dfrac{\sqrt{2}}{2} \right) = -\dfrac{1}{2}.$$
Now substitute $x=\dfrac{\pi}{4}$ into the right-hand side yielding
$$\cos^2 \left( \dfrac{\pi}{4} \right) = \left( \dfrac{\sqrt{2}}{2} \right)^2 = \dfrac{2}{4} = \dfrac{1}{2}.$$
Since $-\dfrac{1}{2} \neq \dfrac{1}{2}$, we must conclude that the given equation is not and identity.
Section 9.2 #7: Find the exact value of $\cos \left( \dfrac{11\pi}{12} \right)$.
Solution: Note that
$$\dfrac{\pi}{6} + \dfrac{3\pi}{4} = \dfrac{2\pi}{12} + \dfrac{9\pi}{12} = \dfrac{11\pi}{12}.$$
Therefore we may apply the sum identity for cosine, i.e.
$$\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)$$
with $\alpha=\dfrac{\pi}{6}$ and $\beta = \dfrac{3\pi}{4}$ to compute
$$\begin{array}{ll}
\cos \left( \dfrac{11\pi}{12} \right) &= \cos \left( \dfrac{\pi}{6} + \dfrac{3\pi}{4} \right) \\
&= \cos \left( \dfrac{\pi}{6} \right) \cos \left( \dfrac{3\pi}{4} \right) - \sin \left( \dfrac{\pi}{6} \right) \sin \left( \dfrac{3\pi}{4} \right) \\
&= \left( \dfrac{\sqrt{3}}{2} \right) \left( -\dfrac{\sqrt{2}}{2} \right) - \left( \dfrac{1}{2} \right) \left( \dfrac{\sqrt{2}}{2} \right) \\
&=\dfrac{-\sqrt{6}-\sqrt{2}}{4}
\end{array}$$
Section 9.2 #11: Rewrite in terms of $\sin(x)$ and $\cos(x)$:
$$\sin \left( x - \dfrac{3\pi}{4} \right).$$
Solution: Using the difference identity for sine, i.e.
$$\sin(\alpha-\beta)=\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)$$
with $\alpha=x$ and $\beta=\dfrac{3\pi}{4}$, we write
$$\begin{array}{ll}
\sin \left( x - \dfrac{3\pi}{4} \right) &= \sin(x) \cos \left( - \dfrac{3\pi}{4} \right) - \cos(x) \sin \left( -\dfrac{3\pi}{4} \right) \\
&= -\dfrac{\sqrt{2}}{2} \sin(x) + \dfrac{\sqrt{2}}{2} \cos(x).
\end{array}$$
Section 9.2 #16: Simplify the expression $\cot \left( \dfrac{\pi}{2} - x \right)$.
Solution: Recall the difference identity for sine (in previous problem) and the difference identity for cosine:
$$\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)$$
with $\alpha=\dfrac{\pi}{2}$ and $\beta=x$. Write
$$\begin{array}{ll}
\cot \left( \dfrac{\pi}{2} - x \right) &= \dfrac{\cos( \frac{\pi}{2}-x)}{\sin(\frac{\pi}{2} - x )} \\
&=\dfrac{\cos(\frac{\pi}{2})\cos(x) + \sin(\frac{\pi}{2})\sin(x)}{\sin(\frac{\pi}{2})\cos(x)-\cos(\frac{\pi}{2})\sin(x)} \\
&= \dfrac{0 \cdot \cos(x) + 1 \cdot \sin(x)}{1 \cdot \cos(x) - 0 \cdot \sin(x)} \\
&= \dfrac{\sin(x)}{\cos(x)} \\
&= \tan(x).
\end{array}$$
Section 9.2 #18: Simplify the expression
$$\sin(2x)\cos(5x) - \sin(5x)\cos(2x).$$
Solution: Recall the difference identity for sine (earlier). The expression in this problem looks like the right-hand side of th diffrence identity for sine with $\alpha=2x$ and $\beta=5x$. Therefore we see that
\begin{array}{ll}
\sin(2x)\cos(5x) - \sin(5x)\cos(2x) &= \sin(2x-5x) \\
&= \sin(-3x) \\
&= -\sin(3x).
\end{array}
Section 9.2 #20: Given that $\sin(a) = \dfrac{2}{3}$ and $\cos(b)=-\dfrac{1}{4}$, with $a$ and $b$ both in the interval $\left[ \dfrac{\pi}{2}, \pi \right)$, find $\sin(a+b)$ and $\cos(a-b)$.
Solution: Note that $a$ and $b$ are both in quadrant II. First we will find $\sin(b)$ and $\cos(a)$. To find $\sin(b)$ consider the following triangle that agrees with $\sin(a)=\dfrac{2}{3}$:
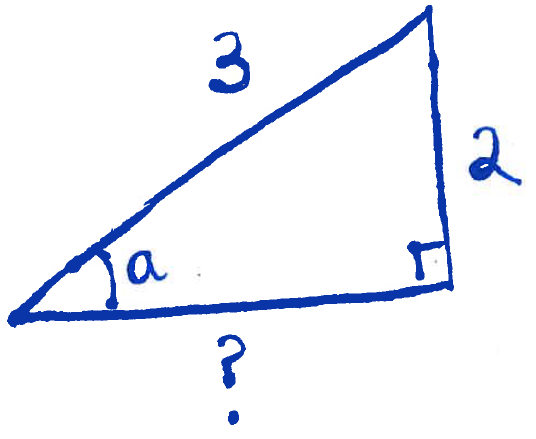and find the missing side labelled "$?$". To do that, use the Pythagorean theorem to write
$$?^2+2^2=3^2,$$
yielding $?=\sqrt{5}$. Therefore $\cos(a)=-\dfrac{\sqrt{5}}{4}$. To find $\cos(a)$ consider the following triangle:
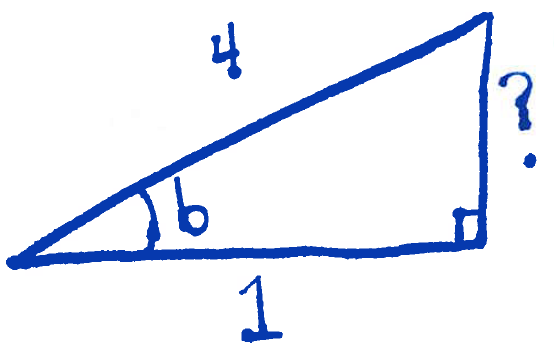and find the missing side labelled "$?$". To do that, use the Pythagorean theorem to write
$$1^2+?^2 = 4^2,$$
yielding $?=\sqrt{15}$. Therefore $\sin(b)=\dfrac{\sqrt{15}}{4}$ (note that sine is positive in quadrant II). Using the sum and difference identities, we compute
$$\begin{array}{ll}
\sin(a+b) &= \sin(a)\cos(b)+\cos(a)\sin(b) \\
&= \left( \dfrac{2}{3} \right) \left( - \dfrac{1}{4} \right) + \left( -\dfrac{\sqrt{5}}{4} \right) \left( \dfrac{\sqrt{15}}{4} \right).
\end{array}$$
and we compute
$$\begin{array}{ll}
\cos(a-b) &= \cos(a)\cos(b) + \sin(a)\sin(b) \\
&= \left( - \dfrac{\sqrt{5}}{4} \right) \left(-\dfrac{1}{4} \right) + \left( \dfrac{2}{3} \right) \left( \dfrac{\sqrt{15}}{4} \right).
\end{array}$$
Section 9.2 #23: Find the exact value of
$$\cos \left( \cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) + \sin^{-1}\left( \dfrac{\sqrt{3}}{2} \right) \right) .$$
Solution: Recall that $\cos^{-1}$ outputs an angle in the range $[0,\pi]$ and $\sin^{-1}$ outputs an angle in the range $\left[ - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right]$. Therefore
$$\cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}$$
and
$$\sin^{-1} \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{3}.$$
Now applying the sum identity for cosine yields
$$\begin{array}{ll}
\cos \left( \cos^{-1} \left( \dfrac{\sqrt{2}}{2} \right) + \sin^{-1} \left( \dfrac{\sqrt{3}}{2} \right) \right) &= \cos \left( \dfrac{\pi}{4} + \dfrac{\pi}{3} \right) \\
&= \cos \left( \dfrac{\pi}{4} \right) \cos \left( \dfrac{\pi}{3} \right) - \sin\left( \dfrac{\pi}{4} \right) \sin \left( \dfrac{\pi}{3} \right) \\
&=\left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{1}{2} \right) - \left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{\sqrt{3}}{2} \right).
\end{array}$$
Section 9.1 #51: Prove the identity
$$\dfrac{\cos(x+h)-\cos(x)}{h} = \cos(x) \dfrac{\cos(h)-1}{h} - \sin(x) \dfrac{\sin(h)}{h}.$$
Solution: Using the sum identity for cosine, compute
$$\begin{array}{ll}
\dfrac{\cos(x+h)-\cos(x)}{h} &= \dfrac{(\cos(x)\cos(h)-\sin(x)\sin(h))-\cos(x)}{h} \\
&= \dfrac{\cos(x)\cos(h)-\cos(x)}{h} - \sin(x) \dfrac{\sin(h)}{h} \\
&= \cos(x) \dfrac{\cos(h)-1}{h} - \sin(x) \dfrac{\sin(h)}{h}.
\end{array}$$
