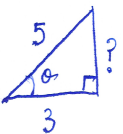Back to the class
Section 8.3 #33: Calculate $\sin \left( \cos^{-1} \left(\dfrac{3}{5} \right) \right)$.
Solution: Let $\theta = \cos^{-1} \left( \dfrac{3}{5} \right)$, and so $\theta$ must lie in QI or QII (because the range of $\cos^{-1}$ is $[0,\pi]$). Taking the cosine of each side yields $\cos(\theta) = \dfrac{3}{5}$, and so $\theta$ must lie in QI or QIV (because the cosine of $\theta$ is a positive number). Therefore $\theta$ lies in QI -- $\sin(\theta)$ is positive.
Draw a right triangle including $\theta$:
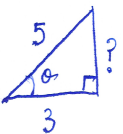Solve for $?$ using the Pythagorean theorem:
$$3^2+?^2=5^2,$$
and hence
$$? = \sqrt{25-9} = \sqrt{16}=4.$$
Now we compute
$$\sin(\theta) = \dfrac{4}{5}.$$
Section 8.3 #34: Calculate $\sin \left( \tan^{-1} \left( \dfrac{4}{3} \right) \right)$.
Solution: Let $\theta=\tan^{-1}\left( \dfrac{4}{3} \right)$, and so $\theta$ must lie in QI or QIV since the range of $\tan^{-1}$ is $\left( -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right)$. Taking tangent of both sides yields $\tan(\theta) = \dfrac{4}{3}$, and so $\theta$ must lie in QI or QIII because tangent is positive. Therefore $\theta$ must lie in QI and so $\sin(\theta)$ is positive.
Draw a right triangle including $\theta$:
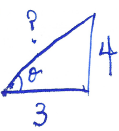Solve for the unknown side $?$ using the Pythagorean theorem:
$$3^2+4^2 = ?^2,$$
and get $?=5$. Now we compute
$$\sin\left( \tan^{-1} \left( \dfrac{4}{3} \right) \right)=\sin(\theta)=\dfrac{4}{5}.$$
Section 8.3 #58: The line $y=\dfrac{3}{5}x$ passes through the origin in the $xy$-plane. What is the measure of the angle that the line makes with the positive $x$-axis?
Solution: Draw this graph and place a point on the graph. For example, if $x=5$ then $y=3$ giving us the point $(5,3)$:
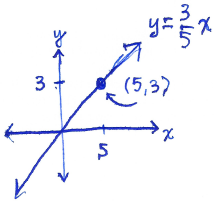The right triangle with bottom leg $5$ and right leg $3$ is clear. If $\theta$ is the angle at the origin, then we see
$$\tan(\theta) = \dfrac{3}{5},$$
hence
$$\theta = \tan^{-1} \left( \dfrac{3}{5} \right) \approx 0.5404 \mathrm{\hspace{2pt} radians}.$$
Section 8.3 #61: A $20$-foot ladder leands up against the side of a building so that the foot of the ladder is $10$ feet from the base of the building. If specifications call for the ladder's angle of elevation to be between $35^{\circ}$ and $45^{\circ}$, does the placement of this ladder satisfy safety specifications?
Solution: Draw this:
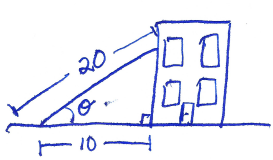From this picture, we see
$$\cos(\theta) = \dfrac{10}{20} = \dfrac{1}{2}.$$
Therefore
$$\theta = \cos^{-1} \left( \dfrac{1}{2} \right) = \dfrac{\pi}{3}=60^{\circ}.$$
Therefore, no, the ladder placement does not obey the specifications.
Section 9.1 #6: Simplify
$$\sin(-x)\cos(-x)\csc(-x).$$
Solution: Using the oddness of sine, i.e. $\sin(-x)=-\sin(x)$, and the evenness of cosine, i.e. $\cos(-x)=\cos(x)$, we see that
$$\begin{array}{ll}
\sin(-x)\cos(-x)\csc(-x) &= \dfrac{\sin(-x)\cos(-x)}{\sin(-x)} \\
&= \dfrac{-\sin(x)\cos(x)}{-\sin(x)} \\
&= \dfrac{\cos(x)}{1} \\
&= \cos(x).
\end{array}$$
Section 9.1 #9: Simplify
$$\dfrac{\cot(t) + \tan(t)}{\sec(-t)}.$$
Solution: Using that cosine is even, calculate
$$\begin{array}{ll}
\dfrac{\cot(t) + \tan(t)}{\sec(-t)} &= \dfrac{\frac{\cos(t)}{\sin(t)} + \frac{\sin(t)}{\cos(t)}}{\frac{1}{\cos(-t)}} \\
&= \dfrac{\frac{\cos^2(t)+\sin^2(t)}{\sin(t)\cos(t)}}{\frac{1}{\cos(t)}} \\
&= \dfrac{1}{\sin(t)\cos(t)} \dfrac{\cos(t)}{1} \\
&= \dfrac{1}{\sin(t)} \\
&= \csc(t).
\end{array}$$
Section 9.1 #10: Simplify
$$3\sin^3(t)\csc(t) + \cos^2(t) + 2\cos(-t)\cos(t).$$
Solution: Using the evenness of cosine, i.e. $\cos(-t)=\cos(t)$, and the Pythagorean identity $\cos^2(t)+\sin^2(t)=1$, calculate
$$\begin{array}{ll}
3\sin^3(t)\csc(t) + \cos^2(t) + 2\cos(-t)\cos(t) &= 3\dfrac{\sin^3(t)}{\sin(t)} + \cos^2(t) + 2\cos^2(t) \\
&= 3\sin^2(t) + \cos^2(t) + 2\cos^2(t) \\
&= 3 \sin^2(t) + 3\cos^2(t) \\
&= 3 ( \cos^2(t) + \sin^2(t)) \\
&= 3.
\end{array}$$
Section 9.1 #18: Simplify the first expression in terms of the second expression:
$$\dfrac{\cos(x)}{1+\sin(x)} + \tan(x); \cos(x).$$
Solution: Calculate
$$\begin{array}{ll}
\dfrac{\cos(x)}{1+\sin(x)} + \tan(x) &= \dfrac{\cos(x)}{1+\sin(x)} + \dfrac{\sin(x)}{\cos(x)} \\
&=\dfrac{\cos^2(x) + \sin(x)(1+\sin(x))}{\cos(x)(1+\sin(x))} \\
&= \dfrac{\cos^2(x)+\sin^2(x)+\sin(x)}{\cos(x)(1+\sin(x))} \\
&= \dfrac{1+\sin(x)}{\cos(x)(1+\sin(x))} \\
&= \dfrac{1}{\cos(x)}.
\end{array}$$
Section 9.1 #19: Simplify the first expression in terms of the second exp
ression:
$$\dfrac{1}{\sin(x)\cos(x)} - \cot(x); \cot(x).$$
Solution: Recall the Pythagorean identity $\cos^2(x)+\sin^2(x)=1$ and rearrange it to get $1-\cos^2(x)=\sin^2(x)$. Now calculate
$$\begin{array}{ll}
\dfrac{1}{\sin(x)\cos(x)} - \cot(x) &= \dfrac{1}{\sin(x)\cos(x)} - \dfrac{\cos(x)}{\sin(x)} \\
&= \dfrac{1-\cos^2(x)}{\sin(x)\cos(x)} \\
&= \dfrac{\sin^2(x)}{\sin(x)\cos(x)} \\
&= \dfrac{\sin(x)}{\cos(x)} \\
&= \tan(x) \\
&= \dfrac{1}{\cot(x)}.
\end{array}$$
