Back to the class
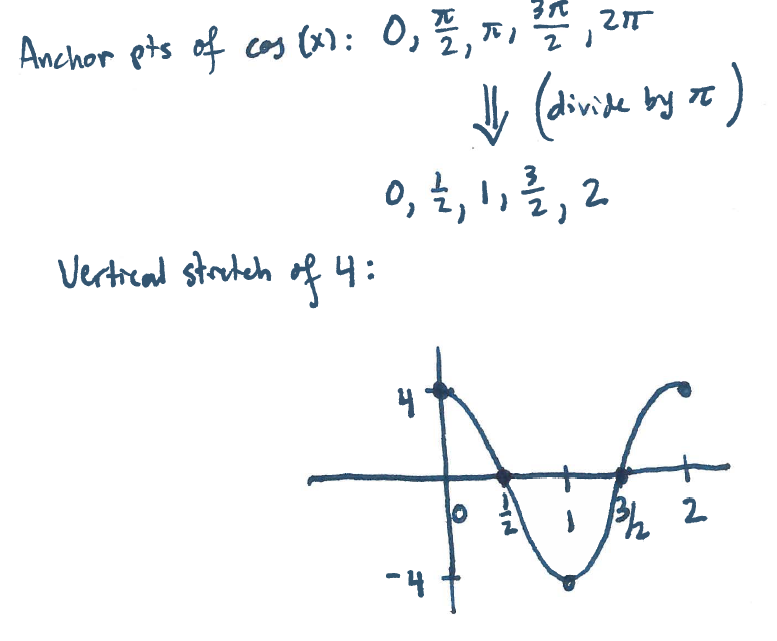
Section 8.1 #13 Plot $f(x)=4\cos \left(\pi x\right)$.
Solution: There is a vertical stretch of $4$ and a horizontal compression by $\pi$ (meaning we divide anchor points by $\pi$):
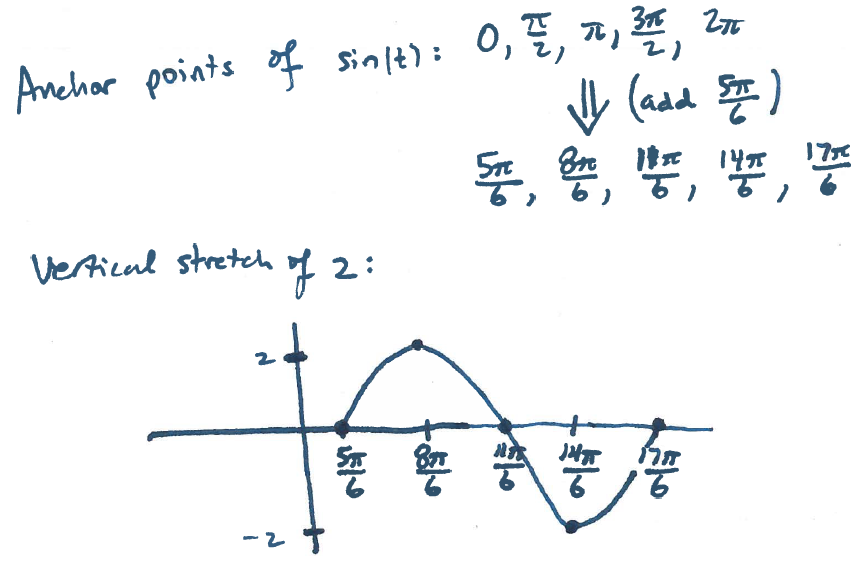
Section 8.1 #18 Plot $f(t)=2\sin \left( t - \dfrac{5\pi}{6} \right)$.
Solution: There is a vertical stretch by $2$ and a horizontal shift right by $\dfrac{5\pi}{6}$:
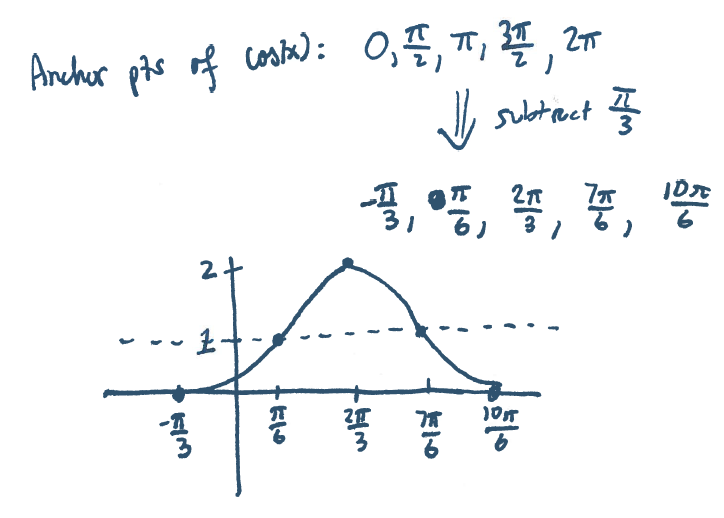
Section 8.1 #19 Plot $f(t)=-\cos \left( t + \dfrac{\pi}{3} \right)+1$.
Solution: There is a vertical reflection, a horizontal shift left by $\dfrac{\pi}{3}$, and a vertical shift up by $1$:
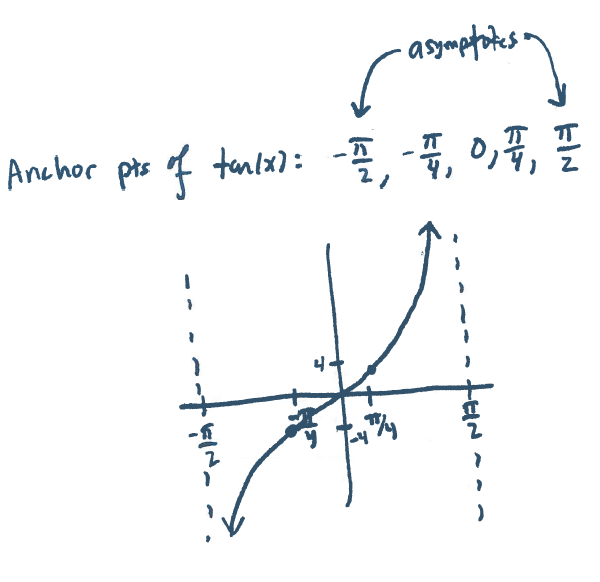
Section 8.2 #24 Plot $f(x)=4\tan(x)$.
Solution: There is a vertical stretch of $4$:
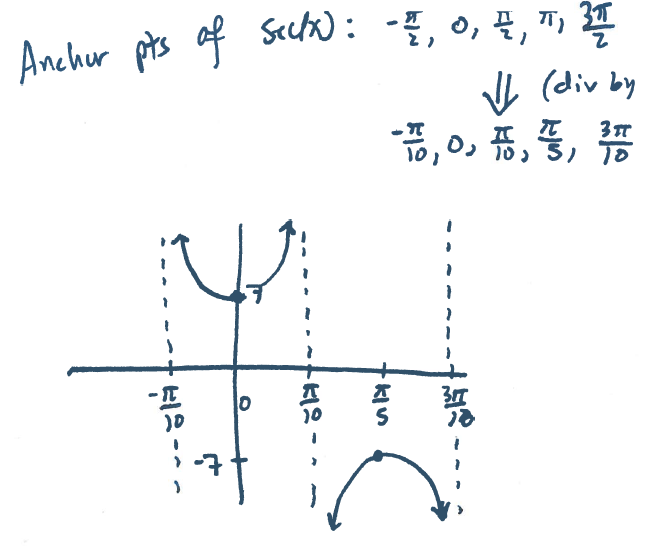
Section 8.2 #31 Plot $f(x)=7\sec(5x)$.
Solution: There is a vertical stretch by $7$ and a horizontal compression by $5$ (meaning we divide $x$-values by $5$):
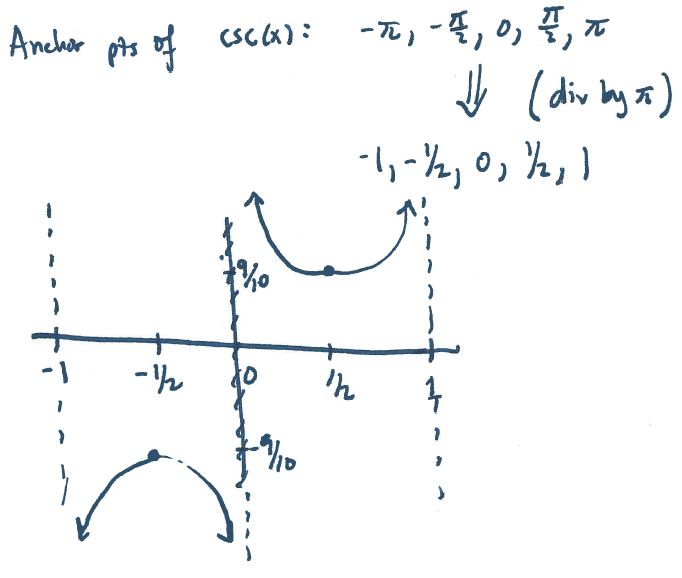
Section 8.2 #32 Plot $f(x)=\dfrac{9}{10} \csc(\pi x)$.
Solution: There is a vertical compression by $\dfrac{9}{10}$ and a horizontal compression by $\pi$ (meaning we divide $x$-values by $\pi$):