Back to the class
Section 7.2 #54: The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.
Solution: Draw the image:
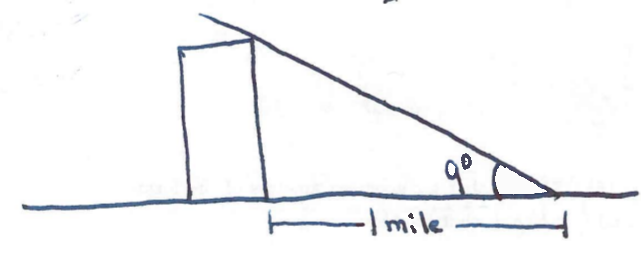
We consider the idealized triangle drawn here:
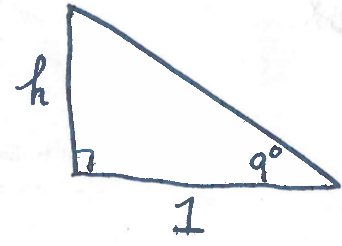
To find the height, use the tangent function to write
$$\tan(9^{\circ})=\dfrac{h}{1}=h.$$
Therefore the height of the building is
$$h=\tan(9^{\circ}) \mathrm{\hspace{2pt} miles} \approx 0.1583 \mathrm{\hspace{2pt} miles}.$$
Since this is an awkward measurement, we may convert miles to feet:
$$0.1583 \mathrm{\hspace{2pt} miles} = 835.82 \mathrm{\hspace{2pt} feet}.$$
Section 7.2 #56: Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be $60^{\circ}$, how far from the base of the tree am I?
Solution: Draw the situation:
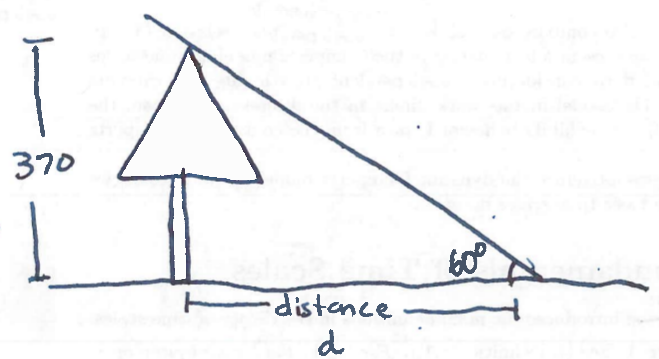
We considser the idealized triangle drawn here:
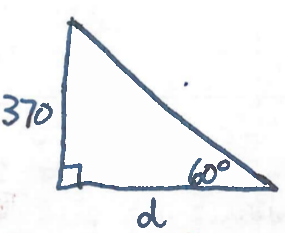
To find the distance $d$, use the tangent function to write
$$\tan(60^{\circ})=\dfrac{370}{d}.$$
Multiply both sides by $d$ and divide by $\tan(60^{\circ})$ to get
$$d = \dfrac{370}{\tan(60^{\circ})} \approx 213.6 \mathrm{\hspace{2pt} feet}. $$
Section 7.4 #74: The equation $P=20\sin(2\pi t)+100$ models the blood pressure, $P$, where $t$ repreesnts time in seconds.
a.) Find the blood pressure after 15 seconds.
b.) What are the maximum and minimum blood pressures?
Solution: For part a.), just plug in $15$ into the function $P$: compute
$$P(15)=20\sin(2 \pi (15))+100 = 100.$$
For part b.), the maximum and minimum blood pressures depend on how large or small the quantity $20 \sin(2\pi t)$ can be. Since the sine function is always between $-1$ and $1$, the smallest value the function $P$ can take is
$$-20+100=80,$$
and the largest value $P$ can take is
$$20+100=120.$$
Section 7.4 #76: The height of a piston, $h$, in inches, can be modeled by the equation $h=2\cos(x)+5$, where $x$ represents the crank angle. Find the height of the piston when the crank angle is $55^{\circ}$.
Solution: Plug in the value $x=55^{\circ}$ into the equation $h=2\cos(x)+5$ to compute the height
$$h=2\cos(55^{\circ})+5 \approx 6.147 \mathrm{\hspace{2pt} inches}.$$






