Back to the class
Section 7.3 #30: State the reference angle for the angle $\dfrac{5\pi}{6}$.
Solution: The angle $\dfrac{5\pi}{6}$ is in quadrant II. To see that, compare to the angle $\dfrac{\pi}{2}=\dfrac{3\pi}{6}$ and $\pi = \dfrac{6\pi}{6}$ ($\dfrac{5\pi}{6}$ is bigger than $\dfrac{3\pi}{6}$ but smaller than $\dfrac{6\pi}{6}$). So, to compute the reference angle for $\dfrac{5\pi}{6}$, we compute the reference angle as
$$\textbf{ref angle}=\pi-\dfrac{5\pi}{6}=\dfrac{\pi}{6},$$
(note: if the angle was in a different quadrant, it would have required a different calculation!). $\blacksquare$
Section 7.3 #52: If $\sin(t)=\dfrac{3}{8}$ and $t$ is in the second quadrant, find $\cos(t)$.
Solution: Since the angle in question is in quadrant II, we must ensure that whatever $\cos(t)$ is, it must be negative. Draw a triangle for this situation, taking the opposite angle of $t$ to be $3$ and the hypotenuse to be $8$:
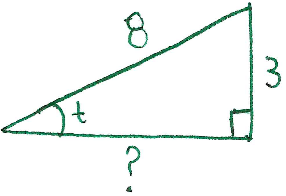Now we find the missing side labelled "$?$" by the Pythagorean theorem:
$$?^2 + 3^2 = 8^2,$$
equivalently,
$$?^2 + 9 = 64.$$
Subtract $9$ from both sides to get
$$?^2=55,$$
and we must conclude that
$$?=\sqrt{55},$$
(note: the negative solution $-\sqrt{55}$ is not considered because $?$ is a length)
From this we may finally conclude that
$$\cos(t) = - \dfrac{\sqrt{55}}{8}. \blacksquare$$
Section 7.3 #70: Find $\sin(t)$ and $\cos(t)$ where $t$ is described by the following unit circle diagram:
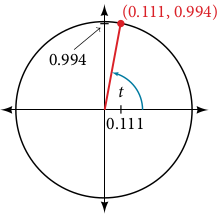
Solution: Since the sine extracts the $y$-coordinate of the point and the cosine extracts the $x$-coordinate of the point, we see that
$$\sin(t)=0.994$$
and
$$\cos(t)=0.111. \blacksquare$$
Section 7.3 #80: Use a calculator to find $\sin \left( \dfrac{5\pi}{9} \right)$.
Solution: (note: make sure your calculator is in radian mode!!)
Calculate
$$\sin \left( \dfrac{5\pi}{9} \right) \approx 0.9848. \blacksquare$$
Section 7.3 #87: Use a calculator to find $\cos \left( 98^{\circ} \right)$.
Solution: (note: make sure your calculator is in degree mode!!)
Calculate
$$\cos \left( 98^{\circ} \right) \approx -0.1391. \blacksquare$$
Section 7.4 #14: Find an exact value for $\tan \left( \dfrac{\pi}{3} \right)$.
Solution: The coordinates on the unit circle corresponding to the angle $\dfrac{\pi}{3}$ are $\left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right)$, and so we calculate
$$\tan \left( \dfrac{\pi}{3} \right) = \dfrac{\sin\left( \dfrac{\pi}{3} \right)}{\cos\left( \dfrac{\pi}{3} \right)}=\dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}. \blacksquare$$
Section 7.4 #21: Find an exact value for the expression $\cot \left( \dfrac{13\pi}{6} \right)$.
Solution: The angle $\dfrac{13\pi}{6}$ is bigger than $2\pi = \dfrac{12\pi}{6}$, so we first subtract $2\pi$ from $\dfrac{13\pi}{6}$ and we see that, as angles,
$$\dfrac{13\pi}{6}=\dfrac{13\pi}{6}-2\pi = \dfrac{13\pi}{6}-\dfrac{12\pi}{6} = \dfrac{\pi}{6}.$$
From this we observe that $\dfrac{13\pi}{6}$ lies in quadrant I and is the same as the angle $\dfrac{\pi}{6}$. Since the coordinates of the point on the unit circle corresponding to angle $\dfrac{\pi}{6}$ are $\left( \dfrac{\sqrt{3}}{2}, \dfrac{1}{2} \right)$, we compute
$$\cot\left( \dfrac{13\pi}{6} \right) = \cot \left( \dfrac{\pi}{6} \right) = \dfrac{\cos\left( \dfrac{13\pi}{6} \right)}{\sin \left( \dfrac{13\pi}{6} \right)} =\dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}. \blacksquare $$
Section 7.4 #39: If $\cos(t)=-\dfrac{1}{3}$ and $t$ is in Quadrant III, find $\sin(t), \sec(t), \csc(t), \tan(t),$ and $\cot(t)$.
Solution: First draw a right triangle with the side adjacent to the angle $t$ being length $1$ and the hypotenuse being length $3$:
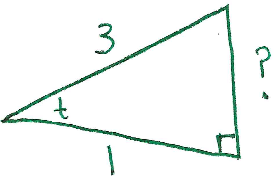Find the missing side labelled "$?$" by using the Pythagorean theorem:
$$3^2+?^2 = 1^2,$$
equivalently
$$9+?^2=1,$$
or
$$?^2=8.$$
Therefore we see that $?=\sqrt{8}$. Since $t$ is in quadrant III, the following trig functions should be positive: $\tan(t)$, $\cot(t)$ and the following trig functions should be negative: $\sin(t), \sec(t), \csc(t)$. Put all the information together to get
$$\sin(t)=-\dfrac{\sqrt{8}}{3},$$
$$\sec(t) = \dfrac{1}{\cos(t)} = \dfrac{1}{-\frac{1}{3}} = -3,$$
$$\csc(t) = \dfrac{1}{\sin(t)} = -\dfrac{3}{\sqrt{8}},$$
$$\tan(t) = \dfrac{\sqrt{8}}{1} = \sqrt{8},$$
and
$$\cot(t) = \dfrac{1}{\tan(t)} = \dfrac{1}{\sqrt{8}}. \blacksquare$$
Section 7.4 #43: If $\sin(t) = \dfrac{\sqrt{2}}{2}$, what is $\sin(-t)$?
Solution: Using the fact that sine is an even function (see pg. 625), we may conclude that
$$\sin(-t) = -\sin(t) = - \dfrac{\sqrt{2}}{2}. \blacksquare$$
