Back to the class
Section 7.2 #6: For the following, use cofunction of complementary angles:
$$\cos(34^{\circ}) = \sin( \underline{\phantom{aaa}}^{\circ}).$$
Solution: By the cofunction identities (Table 1 on page 597) and recalling that $\dfrac{\pi}{2}$ radians is the same as $90^{\circ}$, we see that
$$\cos(34^{\circ}) = \sin \left( 90^{\circ} - 34^{\circ} \right) = \sin \left( 56^{\circ} \right).$$
Section 7.2 #12: Find the missing sides if side $a$ is opposide angle $A$, side $b$ is opposite angle $B$, and side $c$ is the hypotenuse:
$$\tan A = \dfrac{5}{12}, b=6.$$
Solution: First draw the described triangle:
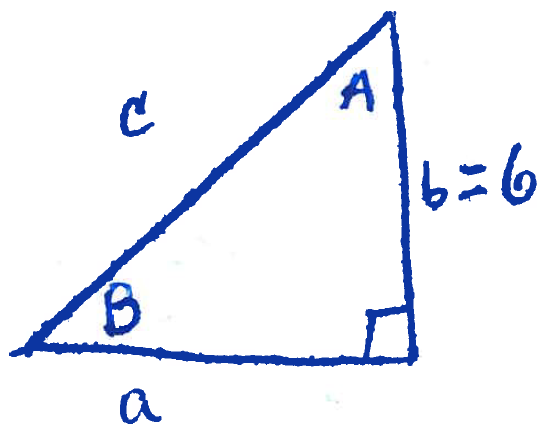By definition, $\tan(A)=\dfrac{a}{b}=\dfrac{a}{6}$ by what we are told. However we are also told that $\tan(A) = \dfrac{5}{12}$. To find $a$ equate these two to see that
$$\dfrac{5}{12} = \tan(A) = \dfrac{a}{6},$$
and solve for $a$ by multiplying by $6$ to get $a = 6\dfrac{5}{12} = \dfrac{5}{2}$. To find the hypotenuse $c$, the Pythagorean theorem tells us that
$$a^2+b^2=c^2,$$
so plug in $a$ and $b$ to get
$$\left( \dfrac{5}{2} \right)^2 + 6^2 = c^2,$$
and simplify the left-hand side to get
$$\dfrac{25}{4} + 36 = c^2,$$
or equivalently
$$\dfrac{25+144}{4} = c^2,$$
or
$$\dfrac{169}{4}=c^2,$$
so that the hypotenuse is
$$c = \sqrt{ \dfrac{169}{4} } = \dfrac{\sqrt{169}}{\sqrt{4}} = \dfrac{13}{2}.$$
(note: we ignored the negative solution because we are solving for the leg of a triangle, a length, which cannot be negative!)
Section 7.2 #18: Evaluate $\cos(A)$ in the following picture:
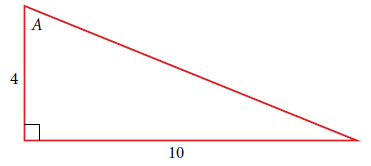
Solution: We must first find the hypotenuse. To do this we will use the Pythagorean theorem. Call the hypotenuse "$?$". Then the Pythagorean theorem says the following equation holds:
$$10^2 + 4^2 = ?^2.$$
Simplify the left hand side to get
$$100 + 16 = ?^2,$$
or equivalently,
$$116 = ?^2.$$
Take square roots to arrive at
$$? = \pm \sqrt{116},$$
but since we are finding the length of a triangle, we do not use the negative solution. Therefore the hypotenuse has length $?=\sqrt{116}$. Now we may answer the question:
$$\cos(A) = \dfrac{\mathrm{adjacent \hspace{2pt} to \hspace{2pt} A}}{\mathrm{hypotenuse}} = \dfrac{4}{\sqrt{116}}.$$
Section 7.2 #30: Solve the following triangle:
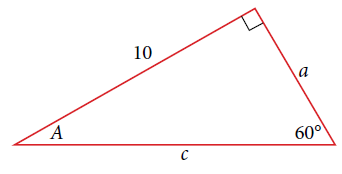
Solution:
Find $A$
Use the fact that sum of the angles in a triangle is $180^{\circ}$ to get the equation
$$A + 60^{\circ} + 90^{\circ} = 180^{\circ}.$$
Simplifying the left-hand side yields
$$A + 150^{\circ} = 180^{\circ}.$$
Subtracting $150^{\circ}$ from both sides yields
$$A = 180^{\circ}-150^{\circ} = 30^{\circ}.$$
Find $a$
To find $a$ we will use the given angle $60^{\circ}$ and the tangent function:
$$\tan(60^{\circ}) = \dfrac{10}{a}.$$
Now multiply both sides by $a$ to get
$$a \tan(60^{\circ}) = 10.$$
To finish, divide both sides by (the number!!) $\tan(60^{\circ})$ to get
$$a = \dfrac{10}{\tan(60^{\circ})}.$$
Find $c$
To find $c$ we will use the given angle $60^{\circ}$ and the sine function:
$$\sin(60^{\circ}) = \dfrac{10}{c}.$$
Now multiply both sides by $c$ to get
$$c\sin(60^{\circ}) = 10.$$
Now divide both sides by (the number!!) $\sin(60^{\circ})$ to get
$$c = \dfrac{10}{\sin(60^{\circ})}.$$
Section 7.2 #36: Solve the triangle and give answers accurate to four decimal places:
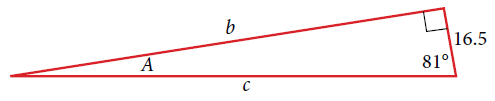
Solution:
Find $A$
Use the fact that the sum of the angles in a triangle is $180^{\circ}$ to write
$$A + 81^{\circ} + 90^{\circ} = 180^{\circ}.$$
Solve that equation to get
$$A = 9^{\circ}.$$
Find $b$
Using the tangent function and the $81^{\circ}$ angle,
$$\tan(81^{\circ}) = \dfrac{b}{16.5}.$$
Solving this for $b$ yields
$$b = 16.5\tan(81^{\circ}) \approx 104.2.$$
Find $c$
Using the cosine function and the $81^{\circ}$ angle,
$$\cos(81^{\circ}) = \dfrac{16.5}{c}.$$
Solving this for $c$ yields
$$c = \dfrac{16.5}{\cos(81^{\circ})} \approx 105.4755.$$
Section 7.2 #48: A $200$-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $15^{\circ}$, and that the angle of depression to the bottom of the tower is $2^{\circ}$. How far is the person from the monument?
Solution: First, draw the described situation:
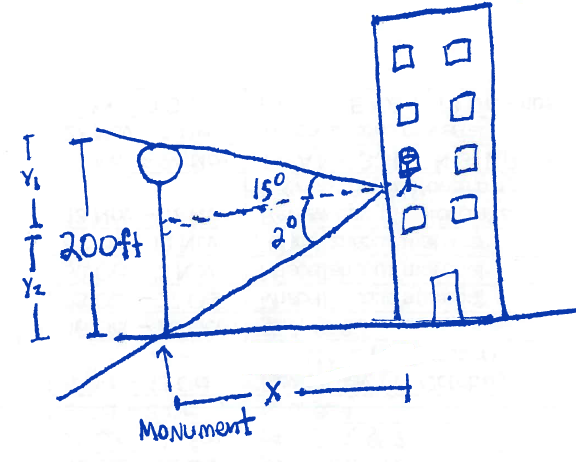This image naturally has two triangles embedded in it which we draw separately to analyze:
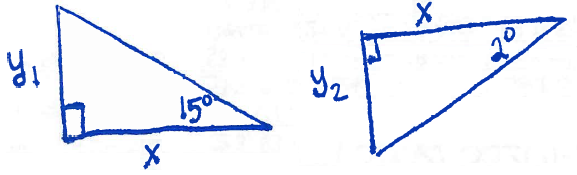We use the variables $y_1$ and $y_2$ because we only know that the height of the monument is $200$ feet, but we don't know the height of the two triangles. That is, we know that
$$(*) \hspace{35pt} y_1+y_2=200.$$
We would like to find $x$. So, seek relationships between all the named sides in each triangle. The first triangle (the one with $15^{\circ}$) obeys
$$\tan(15^{\circ})=\dfrac{y_1}{x},$$
and when algebraically manipulated yields
$$(**) \hspace{35pt} y_1 = x \tan(15^{\circ}).$$
(note: could also solve for $x$ in each triangle and set them equal to do this problem!)
Now in the second triangle,
$$\tan(2^{\circ})=\dfrac{y_2}{x},$$
and so algebra shows
$$(***) \hspace{35pt} y_2 = x \tan(2^{\circ}).$$
By equations $(*)$, $(**)$, and $(***)$, we see that
$$200 = y_1+y_2 = x \tan(15^{\circ}) + x\tan(2^{\circ}).$$
On the right-hand side, factor out $x$ to arrive at the equation
$$200 = x \left[ \tan(15^{\circ}) + \tan(2^{\circ}) \right].$$
Now dividing by the number $\tan(15^{\circ})+\tan(2^{\circ})$ yields the solution
$$x = \dfrac{200}{\tan(15^{\circ})+\tan(2^{\circ})} \approx 660.3.$$
Section 7.2 #50: There is an antenna on the top of a building. From a location $300$ feet from the base of the building, the angle of elevation to the top of the building is measured to be $40^{\circ}$. From the same location, the angle of elevation to the top of the antenna is measured to be $43^{\circ}$. Find the height of the antenna.
Solution: First, draw the situation:
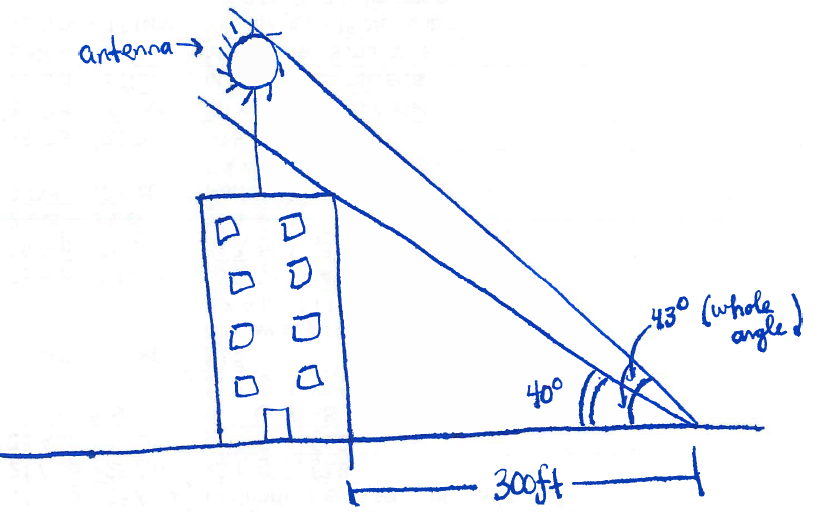Let us call the height of the antenna alone $a$ and the height of the building $b$. Extract the two triangles that appear in the picture:
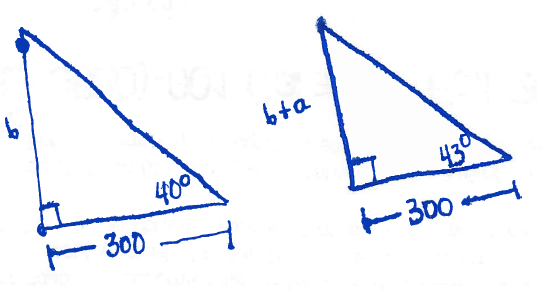Our goal is to find $a$. First let us find the quantity $b$ in the first triangle:
$$\tan(40^{\circ})=\dfrac{b}{300},$$
therefore we see
$$b = 300\tan(40^{\circ}) \approx 251.7 \mathrm{ft}.$$
Now we may solve the second triangle for the height $b+a$:
$$\tan(43^{\circ}) = \dfrac{b+a}{300},$$
therefore we see
$$b+a=300\tan(43^{\circ}) \approx 279.8 \mathrm{ft}.$$
Now combine what we know to see that
$$a = (b+a)-b = 279.8 \mathrm{ft} - 251.7 \mathrm{ft} = 28.1 \mathrm{ft}.$$
Section 7.2 #53: A $23$-ft ladder leans against a building so that the angle between the ground and the ladder is $80^{\circ}$. How high does the ladder reach up the side of the building?
Solution: First, draw this situation:
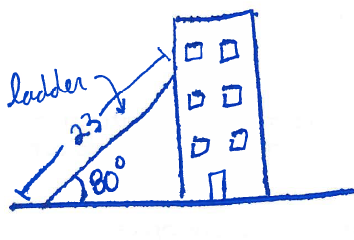Extract the triangle in this picture:
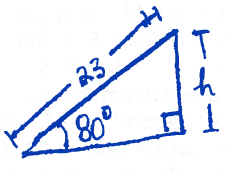We would like to find $h$. To do so, write
$$\sin(80^{\circ}) = \dfrac{h}{23},$$
and so we see
$$h = 23 \sin(80^{\circ}) \approx 22.65.$$
Section 7.3 #6: Use the given sign of the sine and cosine functions to find the quadrant in which the terminal point is detemined by angle $t$ lies:
$\sin(t) < 0$ and $\cos(t) < 0$.
Solution: Since sine corresponds to the $y$-coordinate, to say that $\sin(t) < 0$ means that the $y$-coordintae is negative. Since cosine corresponds to the $x$-coordinate, to say that $\cos(t) < 0$ means that the $x$-coordinate is negative. This means the terminal side of angle $t$ must lie in quadrant III.
Section 7.3 #12: Find an exact value for $\cos \left( \dfrac{\pi}{2} \right)$.
Solution: Since angle $\dfrac{\pi}{2}$ corresponds to the point on the unit circle with coordinates $(0,1)$ and the cosine function reads off the $x$-coordintae, we must conclude that
$$\cos \left( \dfrac{\pi}{2} \right) = x\mathrm{-coordinate \hspace{2pt} of \hspace{2pt}}(0,1) = 0.$$
