Back to the class
Section 4.2 #18: Use the properties of summation and Theorem 4.2 to evaluate the sum
$$\displaystyle\sum_{k=1}^{10} (k^2-1).$$
Solution: Use the property $\sum (f(k)+g(k))=\left( \sum f(k) \right) + \left( \sum g(k) \right)$ to see
$$\displaystyle\sum_{k=1}^{10} (k^2-1) = \left( \displaystyle\sum_{k=1}^{10} k^2 \right) - \left( \displaystyle\sum_{k=1}^{10} 1 \right).$$
Now using Theorem 4.2 (1) and (3), we get
$$\displaystyle\sum_{k=1}^{10} (k^2-1) = \dfrac{10(10+1)(2(10)+1)}{6} - 10 = \dfrac{10(11)(21)}{6}-\dfrac{60}{6} = \dfrac{2250}{6} = \dfrac{1125}{3} = 375.$$
Section 4.2 #26: Use left- and right- endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the $x$-axis:
$$f(x)=9-x, [2,4], 6 \rm{\hspace{2pt} rectangles}.$$
Solution: In this problem we have
$$\Delta x = \dfrac{4-2}{6} = \dfrac{2}{6}=\dfrac{1}{3}.$$
Therefore we get the following picture for left-endpoints:
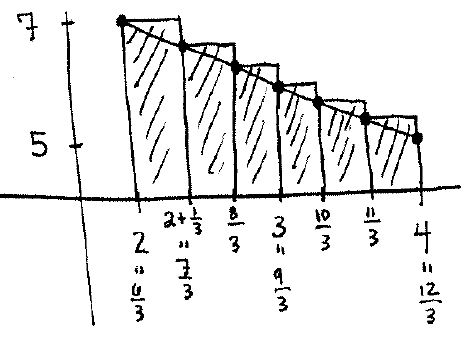
The width of these rectangles are all $\dfrac{1}{3}$ and the height comes from evaluating the function $f(x)=9-x=\dfrac{27}{3}-x$ at each left end point $x_k$:
$$\begin{array}{ll}
\mathrm{Approx \hspace{2pt} area} &= \displaystyle\sum_{k=1}^6 f(x_k)\Delta x \\
&= f \left( \dfrac{6}{3} \right) \dfrac{1}{3} + f \left( \dfrac{7}{3} \right) \dfrac{1}{3} + f \left( \dfrac{8}{3} \right) \dfrac{1}{3} + f \left( \dfrac{9}{3} \right) \dfrac{1}{3} + f \left( \dfrac{10}{3} \right) \dfrac{1}{3} + f \left( \dfrac{11}{3} \right) \dfrac{1}{3} \\
&= \dfrac{21}{3} \dfrac{1}{3} + \dfrac{20}{3} \dfrac{1}{3} + \dfrac{19}{3} \dfrac{1}{3} + \dfrac{18}{3} \dfrac{1}{3} + \dfrac{17}{3} \dfrac{1}{3} + \dfrac{16}{3} \dfrac{1}{3} \\
&= \dfrac{1}{9} \left[ 21 + 20+ 19 + 18 + 17 + 16 \right] \\
&=\dfrac{111}{9} \\
&= \dfrac{37}{3}.
\end{array}$$
We also do a right endpoint approximation:
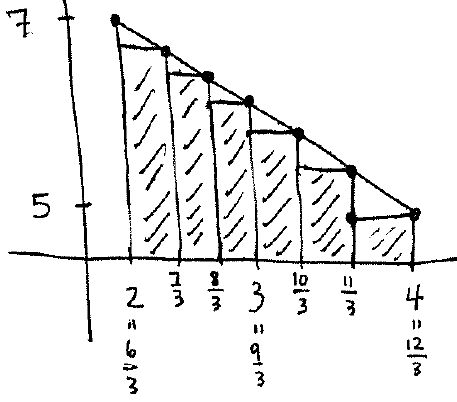
The width of each rectangle is $\dfrac{1}{3}$ and we proceed as we did before using $x_k$ to denote right endpoints to get
$$\begin{array}{ll}
\mathrm{Approx \hspace{2pt} area} &= \displaystyle\sum_{k=1}^6 f(x_k)\Delta x \\
&= f \left( \dfrac{7}{3} \right) \dfrac{1}{3} + f \left( \dfrac{8}{3} \right) \dfrac{1}{3} + f \left( \dfrac{9}{3} \right) \dfrac{1}{3} + f \left( \dfrac{10}{3} \right) \dfrac{1}{3} + f \left( \dfrac{11}{3} \right) \dfrac{1}{3} + f \left( \dfrac{12}{3} \right) \dfrac{1}{3} \\
&= \dfrac{20}{3} \dfrac{1}{3} + \dfrac{19}{3} \dfrac{1}{3} + \dfrac{18}{3} \dfrac{1}{3} + \dfrac{17}{3} \dfrac{1}{3} + \dfrac{16}{3} \dfrac{1}{3} + \dfrac{15}{3} \dfrac{1}{3} \\
&= \dfrac{1}{9} \left[ 20 + 19 + 18 + 17+ 16 + 15 \right] \\
&=\dfrac{105}{9} \\
&= \dfrac{35}{3}.
\end{array}$$
Section 4.2 #37: Find a formula for the sum of $n$ terms. Use the formula to find the limit as $n \rightarrow \infty$:
$$\displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{k=1}^n \dfrac{24k}{n^2}.$$
Solution: Using the property that allows us to pull out things that are constant (with respect to $k$) and Theorem 4.2 (2):
$$\displaystyle\sum_{k=1}^n \dfrac{24k}{n^2} = \dfrac{24}{n^2} \displaystyle\sum_{k=1}^n k = \dfrac{24}{n^2} \dfrac{n(n+1)}{2} = 12 \dfrac{n^2+1}{n^2} = 12 \left( 1 + \dfrac{1}{n^2} \right).$$
Therefore
$$\displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{k=1}^n \dfrac{24k}{n^2} = \displaystyle\lim_{n \rightarrow \infty} 12 \left( 1 + \dfrac{1}{n^2} \right) = 12(1+0) = 12.$$
Section 4.3 #4: Evaluate the definite integral using the limit definition:
$$\displaystyle\int_{-2}^3 x \rm{d}x.$$
Solution: Here we have the interval $[a,b]=[-2,3]$. So, $\Delta x = \dfrac{3-(-2)}{n} = \dfrac{5}{n}.$ This gives us $x_k=-2 + \dfrac{5k}{n}$. Therefore we may compute
$$\begin{array}{ll}
\displaystyle\sum_{k=1}^n f(x_k) \Delta x &= \displaystyle\sum_{k=1}^n \left( -2 + \dfrac{5k}{n} \right) \dfrac{5}{n}\\
&=\dfrac{5}{n} \displaystyle\sum_{k=1}^n\left( -2 + \dfrac{5k}{n} \right) \\
&= \dfrac{5}{n} \left[-2 \left(\displaystyle\sum_{k=1}^n 1 \right) + \dfrac{5}{n} \left( \displaystyle\sum_{k=1}^n k \right) \right] \\
&= \dfrac{5}{n} \left[ -2n + \dfrac{5}{n} \dfrac{n(n+1)}{2} \right] \\
&= -10 + \dfrac{25}{2n^2} (n^2+1) \\
&= -10 + \dfrac{25}{2} \left( 1 + \dfrac{1}{n^2} \right).
\end{array}$$
Therefore by the definition of definite integrals, we get
$$\begin{array}{ll}
\displaystyle\int_{-2}^3 x \rm{d}x &= \displaystyle\lim_{n \rightarrow\infty} \displaystyle\sum_{k=1}^n f(x_k) \Delta x \\
&= \displaystyle\lim_{n \rightarrow \infty} -10+\dfrac{25}{2} \left(1 + \dfrac{1}{n^2} \right) \\
&= -10 + \dfrac{25}{2} (1+ 0) \\
&= -\dfrac{20}{2} + \dfrac{25}{2} \\
&= \dfrac{5}{2}.
\end{array}$$
Section 4.3 #6: Evaluate the definite integral using the limit definition:
$$\displaystyle\int_1^4 4x^2 \rm{d}x.$$
Solution: Here $[a,b]=[1,4]$ and so $\Delta x = \dfrac{4-1}{n}=\dfrac{3}{n}$ and $x_k = 1+ \dfrac{3k}{n}$. Notice that
$$\begin{array}{ll}
\displaystyle\sum_{k=1}^n f(x_k)\Delta x &= \displaystyle\sum_{k=1}^n 4\left(1+\dfrac{3k}{n} \right)^2 \dfrac{3}{n} \\
&=\dfrac{12}{n} \displaystyle\sum_{k=1}^n \left( 1 + \dfrac{3k}{n} \right)^2 \\
&= \dfrac{12}{n} \displaystyle\sum_{k=1}^n \left( 1 + \dfrac{6k}{n} + \dfrac{9k^2}{n^2} \right) \\
&=\dfrac{12}{n} \left[ \left( \displaystyle\sum_{k=1}^n 1 \right) + \dfrac{6}{n} \left( \displaystyle\sum_{k=1}^n k \right) + \dfrac{9}{n^2} \left( \displaystyle\sum_{k=1}^n k^2 \right) \right] \\
&= \dfrac{12}{n} \left[ n + \dfrac{6}{n} \left( \dfrac{n(n+1)}{2} \right) + \dfrac{9}{n^2} \left(\dfrac{n(n+1)(2n+1)}{6} \right) \right] \\
&= 12 + \dfrac{72}{2} \dfrac{n+1}{n} + \dfrac{36}{2} \dfrac{(n+1)(2n+1)}{n^2} \\
&= 12 + 36 \left( 1 + \dfrac{1}{n} \right) + 18 \dfrac{2n^2+3n+1}{n^2} \\
&= 12 + 36 \left( 1 + \dfrac{1}{n} \right) + 18 \left( 2 + \dfrac{3}{n} + \dfrac{1}{n^2} \right) \\
\end{array}$$
Therefore by the definition of definite integrals, we get
$$\begin{array}{ll}
\displaystyle\int_1^4 4x^2 \rm{d}x &= \displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{k=1}^n f(x_k) \Delta x \\
&= \displaystyle\lim_{n \rightarrow \infty} \left( 12 + 36 \left( 1 + \dfrac{1}{n} \right) + 18 \left( 2 + \dfrac{3}{n} + \dfrac{1}{n^2} \right) \right) \\
&= 12 + 36 ( 1+0) + 18(2+0+0) \\
&= 12 + 36 + 36 \\
&= 84.
\end{array}$$




