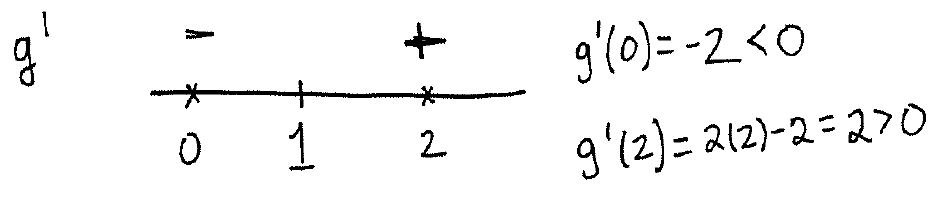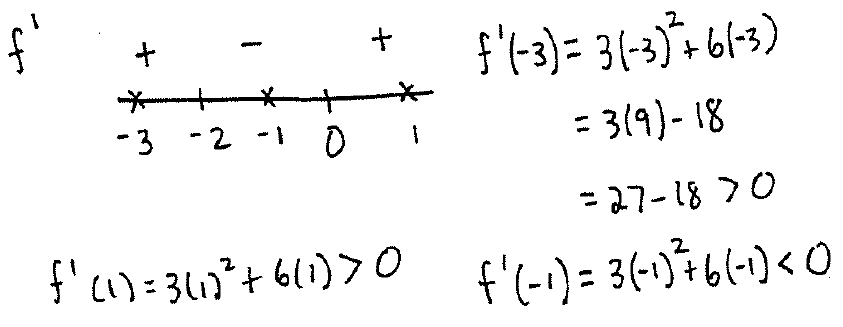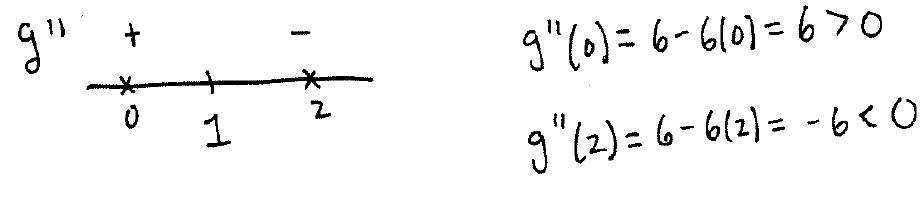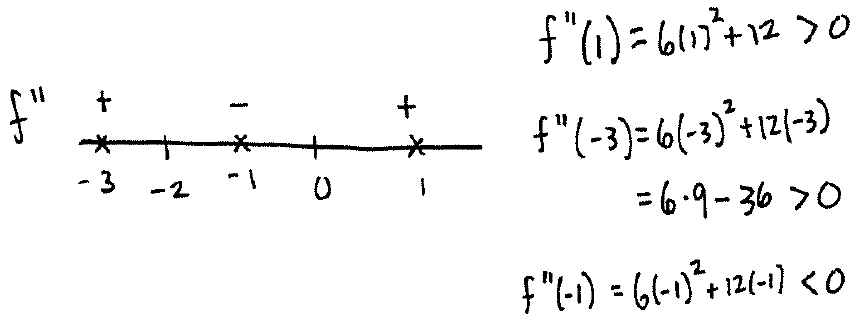Back to the class
Section 3.3 #9: Identify the open intervals where the function is increasing and where the function is decreasing:
$$g(x)=x^2-2x-8.$$
Solution: Find the critical points:
$$g'(x)=2x-2 \stackrel{\mathrm{set}}{=}0.$$
Solving this equation yields $x=1$. Now make a diagram:
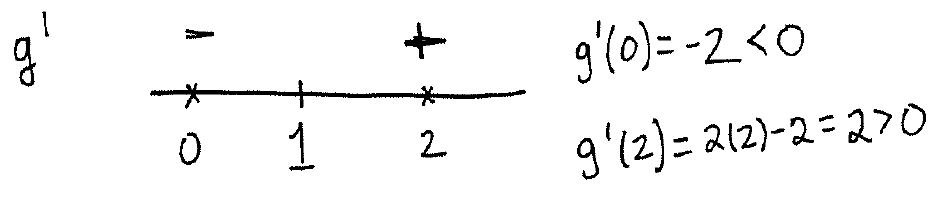
From this diagram we may conclude that the function is increasing on the interval $(1,\infty)$ and it is decreasing on the interval $(-\infty,1)$.
Section 3.3 #24: Use the first derivative test to find the relative extrema of
$$f(x)=(x+2)^2(x-1).$$
Solution: Find the critical points:
$$\begin{array}{ll}
f'(x)&=2(x+2)(x-1) + (x+2)^2 \\
&=2(x^2+x-2)+(x^2+4x+4)\\
&=3x^2+6x \stackrel{\mathrm{set}}{=} 0.
\end{array}$$
To solve $3x^2+6x=0$, factor out $3x$ to get $3x(x+2)=0$. We get the critical points $x=0,-2$. Now make a diagram:
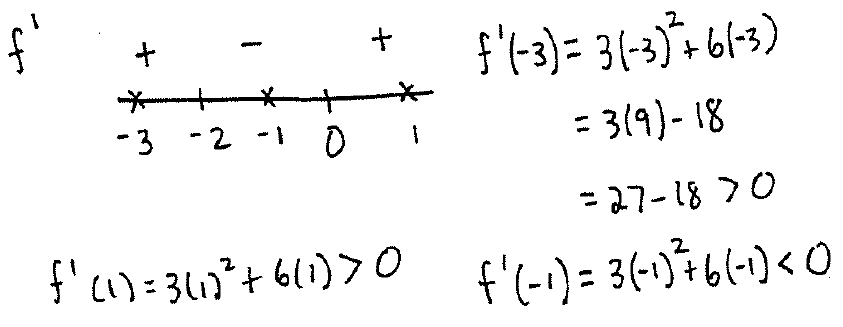
From the diagram, we see there is a relative maximum at $x=-2$ and a relative minimum at $x=0$.
Section 3.4 #4: Determine the open intervals where the function is concave up and where the function is concave down:
$$g(x)=3x^2-x^3.$$
Solution: Find the second derivative and possible inflection points:
$$g'(x)=6x-3x^2$$
and
$$g''(x)=6-6x \stackrel{\mathrm{set}}{=}0.$$
Find the possible inflection point by solving $6-6x=0$ to get $x=1$. Now make a diagram:
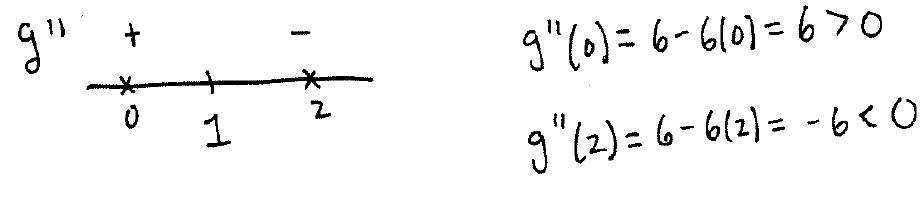
From the diagram, we see the graph is concave up on $(-\infty,1)$ and concave down on $(1,\infty)$.
Section 3.4 #17: Find the point(s) of inflection and discuss the concavity of the graph of the function
$$f(x)=\dfrac{x^4}{2}+2x^3.$$
Solution: Find the second derivative and possible inflection points:
$$f'(x)=2x^3+6x^2,$$
$$f''(x)=6x^2+12x \stackrel{set}{=}0.$$
Solve $6x^2+12x=0$ by factoring out an $x$ to get $x(6x+12)=0$. This has solution $x=0,-2$. Now make a diagram:
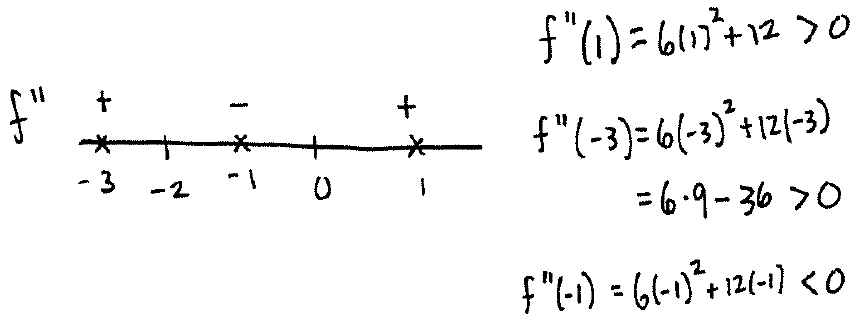
From the diagram, we see that the graph is concave up on $(-\infty,-3)$ and $(0,\infty)$ and concave down on $(-2,0)$. Also there is an inflection point at $x=-2$ and $x=0$.
Section 3.4 #39: Use the second derivative test to find the relative extrema of
$$f(x)=x + \dfrac{4}{x}.$$
Solution: Find the critical points:
$$f'(x) = 1 - \dfrac{4}{x^2} \stackrel{\mathrm{set}}{=} 0.$$
This yields the equation (for $x \neq 0$)
$$1 = \dfrac{4}{x^2}.$$
Multiply by $x^2$ to get
$$x^2 = 4,$$
and take square root to get the critical points
$$x = \pm 2.$$
Find the second derivative:
$$f''(x)=\dfrac{8}{x^3}.$$
To use the second derivative test, plug the critical points into $f''$:
$$f''(-2) = \dfrac{8}{(-2)^3} = \dfrac{8}{-8} = -1 < 0,$$
from which we can conclude that $f$ has a relative max at $x=-2$, and
$$f''(2)=\dfrac{8}{2^3}=\dfrac{8}{8} = 1 > 0,$$
from which we can conclude that $f$ has a relative min at $x=2$.