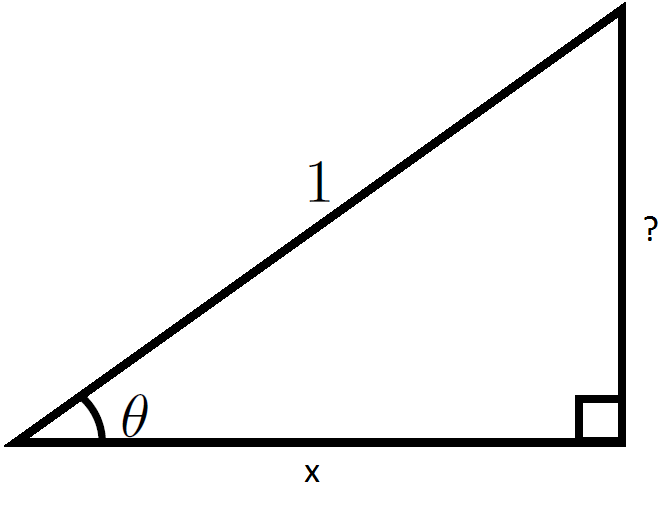Back to the class
A.) Use implicit differentiation and basic trigonometry to find $\dfrac{\mathrm{d}}{\mathrm{d}x} \mathrm{arccos}(x)$ where $\mathrm{arccos}$ denotes the inverse cosine function.
Solution: Since inverse trig functions output angles, let us write $\theta=\arccos(x)$. Consequently,
$$\cos(\theta)=x.$$
This means that
$$\dfrac{\mathrm{d}\theta}{\mathrm{d}x}=\dfrac{\mathrm{d}}{\mathrm{d}x} \mathrm{arccos}(x).$$
Since the derivative of $\cos(x)$ is $-\sin(x)$, implicit differentiation shows that
$$-\sin(\theta) \dfrac{\mathrm{d}\theta}{\mathrm{d}x} = 1,$$
and so we see
$$\dfrac{\mathrm{d}\theta}{\mathrm{d}x} = \dfrac{-1}{\sin(\theta)}.$$
To complete the problem, we must determine how to express $\sin(\theta)$ in terms of the variable $x$. Since we already know that $\cos(\theta)=x$, remembering the fact from right triangle trigonometry that the cosine of an angle is the "adjacent divided by the hypotenuse", we may draw the following picture:
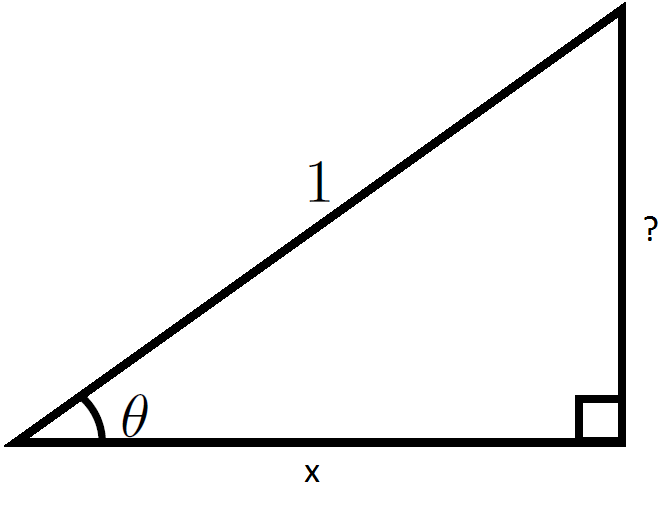
Remembering that $\sin(\theta)$ is the "opposite divided by the hypotenuse" means we need to find the length of the missing side. Call the unknown length $?$. The Pythagorean theorem tells us that
$$?^2 + x^2 = 1^2.$$
Solving for $?$ yields
$$? = \pm \sqrt{1-x^2}.$$
Since the length of the side of a triangle cannot be negative, we must take the value
$$? = \sqrt{1-x^2}.$$
This completes the triangle and so we see that
$$\sin(\theta) = \dfrac{\sqrt{1-x^2}}{1} = \sqrt{1-x^2}.$$
Therefore we get
$$\dfrac{\mathrm{d}}{\mathrm{d}x} \mathrm{arccos}(x) = \dfrac{\mathrm{d}\theta}{\mathrm{d}x} = -\dfrac{1}{\sin(\theta)} = -\dfrac{1}{\sqrt{1-x^2}}.$$
Section 2.5 #5: Find $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ from the following equation:
$$x^3-xy+y^2=7.$$
Solution: Differentiate on both sides (differentiating implicitly where appropriate) to get
$$3x^2 - \left(y + x \dfrac{\mathrm{d}y}{\mathrm{d}x} \right) + 2y\dfrac{\mathrm{d}y}{\mathrm{d}x} = 0.$$
Take the terms that have no $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ in them to the other side to get
$$-x \dfrac{\mathrm{d}y}{\mathrm{d}x}+2y \dfrac{\mathrm{d}y}{\mathrm{d}x} = - 3x^2 + y.$$
Factor the $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ in the left side and then divide to get
$$\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{-3x^2+y}{2y-x}.$$
Section 2.5 #39: Find an equation of the tangent line to the lemniscate
$$3(x^2+y^2)^2 = 100 (x^2-y^2)$$
at the point $(4,2)$.
Solution: Differentiate implicitly (note there is an extra chain rule on the left!) to get
$$6(x^2+y^2) \left(2x + 2y \dfrac{\mathrm{d}y}{\mathrm{d}x} \right) = 100 \left( 2x - 2y \dfrac{\mathrm{d}y}{\mathrm{d}x} \right).$$
Take all the terms with a $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ in them to the left side and everything else to the right side:
$$12y(x^2+y^2) \dfrac{\mathrm{d}y}{\mathrm{d}x}+200y \dfrac{\mathrm{d}y}{\mathrm{d}x} = 200x - 12x(x^2+y^2).$$
Now solve for $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ to get
$$\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{200x - 12x(x^2+y^2)}{12y(x^2+y^2)+200y}=\dfrac{x(50-3x^2-3y^2)}{y(50+3x^2+3y^2)}.$$
We get the slope of the tangent line by plugging in the point $(4,2)$ into this formula, i.e. $x=4$ and $y=2$:
$$\mathrm{slope}=\dfrac{\mathrm{d}y}{\mathrm{d}x} \Bigg|_{x=4,y=2} = \dfrac{4(50-3\cdot 16 - 3 \cdot 4)}{2(50 + 3 \cdot 16 + 3 \cdot 4)}=-\dfrac{2}{11}.$$
Therefore using the point-slope form of the equation of a line, i.e. $y-y-1=m(x-x_1)$ using the point $(4,2)$, we get
$$y-2=-\dfrac{2}{11} (x-4).$$
Indeed, this answer is worth full credit, but you could also put this in $y=mx+b$ form to get
$$y=- \dfrac{2x}{11}+\dfrac{30}{11}.$$
Section 2.6 #11: The radius $r$ of a circle is increasing at a rate of $4$ centimeters per minute. Find the rates of change of the area when
a.) $r=8$ centimeters
b.) $r=32$ centimeters
Solution:
Variables: $r$ -- radius of circle, $A$ -- area of circle
Known rate: $\dfrac{\mathrm{d}r}{\mathrm{d}t}=4 \dfrac{\mathrm{cm}}{\mathrm{min}}$
Equation: Area equation of circle: $A = \pi r^2$
We seek: $\dfrac{\mathrm{d}A}{\mathrm{d}t}$ when $r=8$ (part a) and when $r=32$ (part b).
Differentiate the equation for area to get
$$\dfrac{\mathrm{d}A}{\mathrm{d}t} = 2\pi r \dfrac{\mathrm{d}r}{\mathrm{d}t}.$$
part a.) To find $\dfrac{\mathrm{d}A}{\mathrm{d}t}$ when $r=8$, plug the known rate $\dfrac{\mathrm{d}r}{\mathrm{d}t}$ and $r=8$ into the equation to get
$$\dfrac{\mathrm{d}A}{\mathrm{d}t} = 2 \pi (8) (4) = 64 \pi \dfrac{\mathrm{cm}^2}{\mathrm{min}}.$$
part b.) To find $\dfrac{\mathrm{d}A}{\mathrm{d}t}$ when $r=32$, plug the known rate $\dfrac{\mathrm{d}r}{\mathrm{d}t}$ and $r=32$ into the equation to get
$$\dfrac{\mathrm{d}A}{\mathrm{d}t}=2 \pi (32)(4) = 256\pi \dfrac{\mathrm{cm}^2}{\mathrm{min}}.$$
Section 2.5 #35: The combined electrical resistance $R$ of two resistors $R_1$ and $R_2$, connected in parallel, is given by
$$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2},$$
where $R, R_1,$ and $R_2$ are measured in ohms. $R_1$ and $R_2$ are increasing at a rate of $1$ and $1.5$ ohms per second, respectively. At what rate is $R$ changing when $R_1=50$ ohms and $R_2=75$ ohms?
Solution:
Variables: $R$ -- resistance, $R_1$ -- first resistor, $R_2$ -- second resistor
Known rates: $\dfrac{\mathrm{d}R_1}{\mathrm{d}t}=1 \dfrac{\mathrm{ohm}}{\mathrm{sec}}$ and $\dfrac{\mathrm{d}R_1}{\mathrm{d}t}=1.5 \dfrac{\mathrm{ohm}}{\mathrm{sec}}$
Equation: we are told the equation in this problem: $\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$
We seek: $\dfrac{\mathrm{d}R}{\mathrm{d}t}$ when $R_1=50$ and $R_2=75$
Recall that $\dfrac{\mathrm{d}}{\mathrm{d}x} \dfrac{1}{x} = -\dfrac{1}{x^2}$, we differentiate our equation (implicitly) and get
$$-\dfrac{1}{R^2} \dfrac{\mathrm{d}R}{\mathrm{d}t} = -\dfrac{1}{R_1^2} \dfrac{\mathrm{d}R_1}{\mathrm{d}t} - \dfrac{1}{R_2^2} \dfrac{\mathrm{d}R_2}{\mathrm{d}t}.$$
We know the two rates $\dfrac{\mathrm{d}R_1}{\mathrm{d}t}=1$ and $\dfrac{\mathrm{d}R_2}{\mathrm{d}t}=1.5$. We are told to use $R_1=50$ and $R_2=75$. Plugging all this information in yields
$$(*) \hspace{40pt} -\dfrac{1}{R^2} \dfrac{\mathrm{d}R}{\mathrm{d}t} = -\dfrac{1}{50^2} (1) - \dfrac{1}{75^2} (1.5).$$
Notice that we are not told the value of $R$ in this problem. To find it, we must use the equation $\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$ and solve for $R$ to get
$$R = \dfrac{1}{\frac{1}{R_1} + \frac{1}{R_2}}.$$
Plugging in $R_1=50$ and $R_2=75$, arithmetic shows us that
$$R = \dfrac{1}{\frac{1}{50} + \frac{1}{75}} = 30.$$
Finally, plug in this value of $R$ into the equation $(*)$ to get
$$-\dfrac{1}{30^2} \dfrac{\mathrm{d}R}{\mathrm{d}t} = -\dfrac{1}{50^2} - \dfrac{1.5}{75^2}.$$
Solve for $\dfrac{\mathrm{d}R}{\mathrm{d}t}$ by multiplying by $-30^2$ to get
$$\dfrac{\mathrm{d}R}{\mathrm{d}t} = \dfrac{30^2}{50^2} + \dfrac{1.5(30^2)}{75^2} = \dfrac{3}{5} \dfrac{\mathrm{ohm}}{\mathrm{sec}}= 0.6 \dfrac{\mathrm{ohm}}{\mathrm{sec}}.$$