Back to the class
Section 1.2, #23: Use the graph of the function $f$ to decide whether the value of the given quantity exists. If it does, find it. If not, explain why:
a.) $f(1)$
b.) $\displaystyle\lim_{x \rightarrow 1} f(x)$
c.) $f(4)$
d.) $\displaystyle\lim_{x \rightarrow 4} f(x)$
The graph of $f$ is shown below:
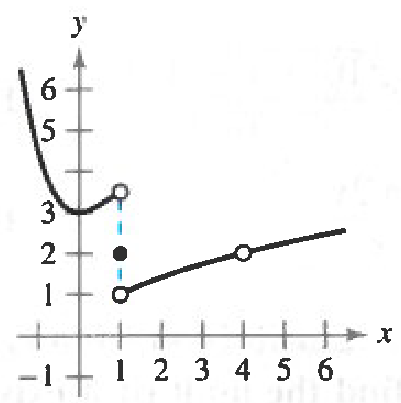
Solution: For part a.), we are being asked if $f(1)$ is defined. This is the case because the closed dot lying above the $x$-value $1$ is filled in. The value of $f(1)$ is simply the height of the dot that is filled in above the $x$-value $1$. So in this case the quantity $f(1)$ exists and observing the graph we see $f(1)=2$.
For part b.), we are asked whether the limit as $x$ approaches $1$ of $f(x)$ exists or not. It does not exist in this case because when approaching $x=1$ from the left, the height of the function approaches approximately $3.5$ while when approaching $x=1$ from the right, the height of the function approaches $1$. Since the limit from the left and the limit from the right disagree, we must say that $\displaystyle\lim_{x \rightarrow 1} f(x)$ does not exist.
For part c.), we are asked if $f(4)$ is defined. This is not the case here because there is no filled in dot lying aanywhere above $x=4$. Hence we would say that $f(4)$ is undefined.
For part d.), we are asked whether or not the limit $\displaystyle\lim_{x \rightarrow 4} f(x)$ exists or not. In this case notice that from both the right and the left, the graph of the function is getting close to the height of the hole. The height of that hole is $2$ and so we will say that $\displaystyle\lim_{x \rightarrow 4} f(x)$ exists and $\displaystyle\lim_{x \rightarrow 4} f(x)=2$. $\blacksquare$
Section 1.3, #50: Compute the limit
$$\displaystyle\lim_{x \rightarrow 5} \dfrac{5-x}{x^2-25}.$$
Solution: Notice that simple substitution of $x=5$ into $\dfrac{5-x}{x^2-25}$ yields indeterminate form $\dfrac{0}{0}$, so there is more work to do. Here use algbra to simplify:
$$\dfrac{5-x}{x^2-25} = \dfrac{5-x}{(x-5)(x+5)} = \dfrac{-(x-5)}{(x-5)(x+5)} = \dfrac{-1}{x+5}.$$
Therefore we see
$$\displaystyle\lim_{x \rightarrow 5} \dfrac{5-x}{x^2-25} = \displaystyle\lim_{x \rightarrow 5} \dfrac{-1}{x+5} = -\dfrac{1}{10}. \blacksquare$$
$\textbf{Section 1.3, #53:}$ Compute the limit
$$\displaystyle\lim_{x \rightarrow 4} \dfrac{\sqrt{x+5}-3}{x-4}.$$
Solution: Notice that simple substitution of $x=4$ into $\dfrac{\sqrt{x+5}-3}{x-4}$ yields indeterminate form $\dfrac{0}{0}$, so there is more work to do. Here use algebra to simplify:
$$\begin{array}{ll}
\dfrac{\sqrt{x+5}-3}{x-4} &= \dfrac{\sqrt{x+5}-3}{x-4} \left( \dfrac{\sqrt{x+5}+3}{\sqrt{x+5}+3} \right) \\
&= \dfrac{(x+5) - 9}{(x-4)(\sqrt{x+5}+3)} \\
&= \dfrac{x-4}{(x-4) (\sqrt{x+5}+3)} \\
&= \dfrac{1}{\sqrt{x+5}+3}.
\end{array}$$
Therefore we see:
$$\displaystyle\lim_{x \rightarrow 4} \dfrac{\sqrt{x+5}-3}{x-4} = \displaystyle\lim_{x \rightarrow 4} \dfrac{1}{\sqrt{x+5}+3} = \dfrac{1}{\sqrt{9}+3} = \dfrac{1}{6}. \blacksquare$$
$\textbf{Section 1.3, #60:}$ Compute the limit
$$\displaystyle\lim_{\Delta x \rightarrow 0} \dfrac{(x+\Delta x)^2-x^2}{\Delta x}.$$
Solution: Notice that simple substitution of $\Delta x=0$ yields indeterminate form $\dfrac{0}{0}$, so there is more work to do. Compute
$$\dfrac{(x+\Delta x)^2-x^2}{\Delta x} = \dfrac{x^2 + 2x \Delta x + (\Delta x)^2 - x^2}{\Delta x} = \dfrac{2x \Delta x + (\Delta x)^2}{\Delta x} = 2x+\Delta x.$$
Therefore compute (note: in the link I use "$h$" instead of $\Delta x$ -- the calculator doesn't like $\Delta x$ too much but this is exactly the same thing....it's just a variable!):
$$\displaystyle\lim_{\Delta x \rightarrow 0} \dfrac{(x+\Delta x)^2-x^2}{\Delta x}=\displaystyle\lim_{\Delta x \rightarrow 0} 2x+\Delta x=2x. \blacksquare$$



