Back to the class
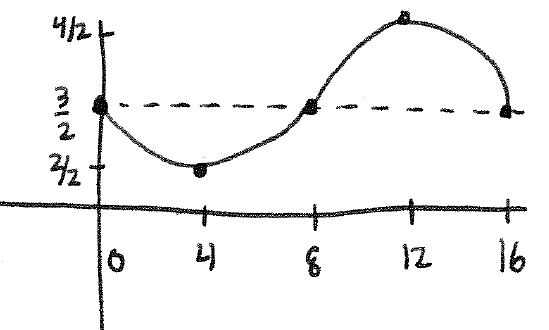
Section 2.4 #58: Graph $y=-\dfrac{1}{2} \sin \left( \dfrac{\pi}{8} x \right) + \dfrac{3}{2}$.
Solution: In this problem, the amplitude is $\dfrac{1}{2}$, the period change is to divide by $\dfrac{\pi}{8}$, and the vertical shift is $\dfrac{3}{2}$ up. This yields the following graph (take care with the minus sign in the front!):
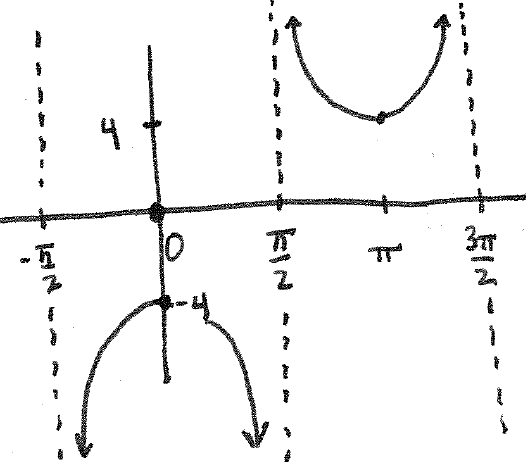
Section 2.5 #28: Graph $y=-4\sec(x)$.
Solution: Graph directly, taking care of the heights at $0$ and $\pi$ and the negative sign in the front yields the graph
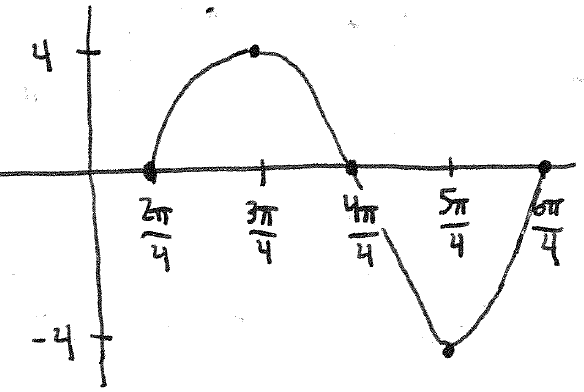
Section 2.6 #3: Graph $y=4\sin(2x-\pi)$.
Solution: Here the amplitude is $4$, the period change is to divide by $2$, and the phase shift is to move $\dfrac{\pi}{2}$ to the right. This yields
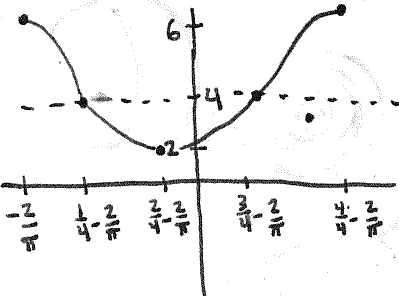
Section 2.6 #10: Graph $y=2 \cos(2\pi x+4) +4$.
Solution: Here the amplitude is $2$, the period change is to divide by $2 \pi$, the phase shift is $\dfrac{4}{2\pi}=\dfrac{2}{\pi}$ to the left, and the vertical shift is $4$ up. This yields: