Back to the class
1. Find the largest domain in the real numbers of the function described by $f(x)=\dfrac{5}{x-7}$.
Solution: The domain is $\mathbb{R} \setminus \{7\}$. You can also describe it in the following ways: "$-\infty < x < 7$ or $7 < x < \infty$" or "$(-\infty,7) \cup (7,\infty)$" or "all real numbers except for $7$")
2. Find the domain and range of the function whose graph is given by the following drawing:
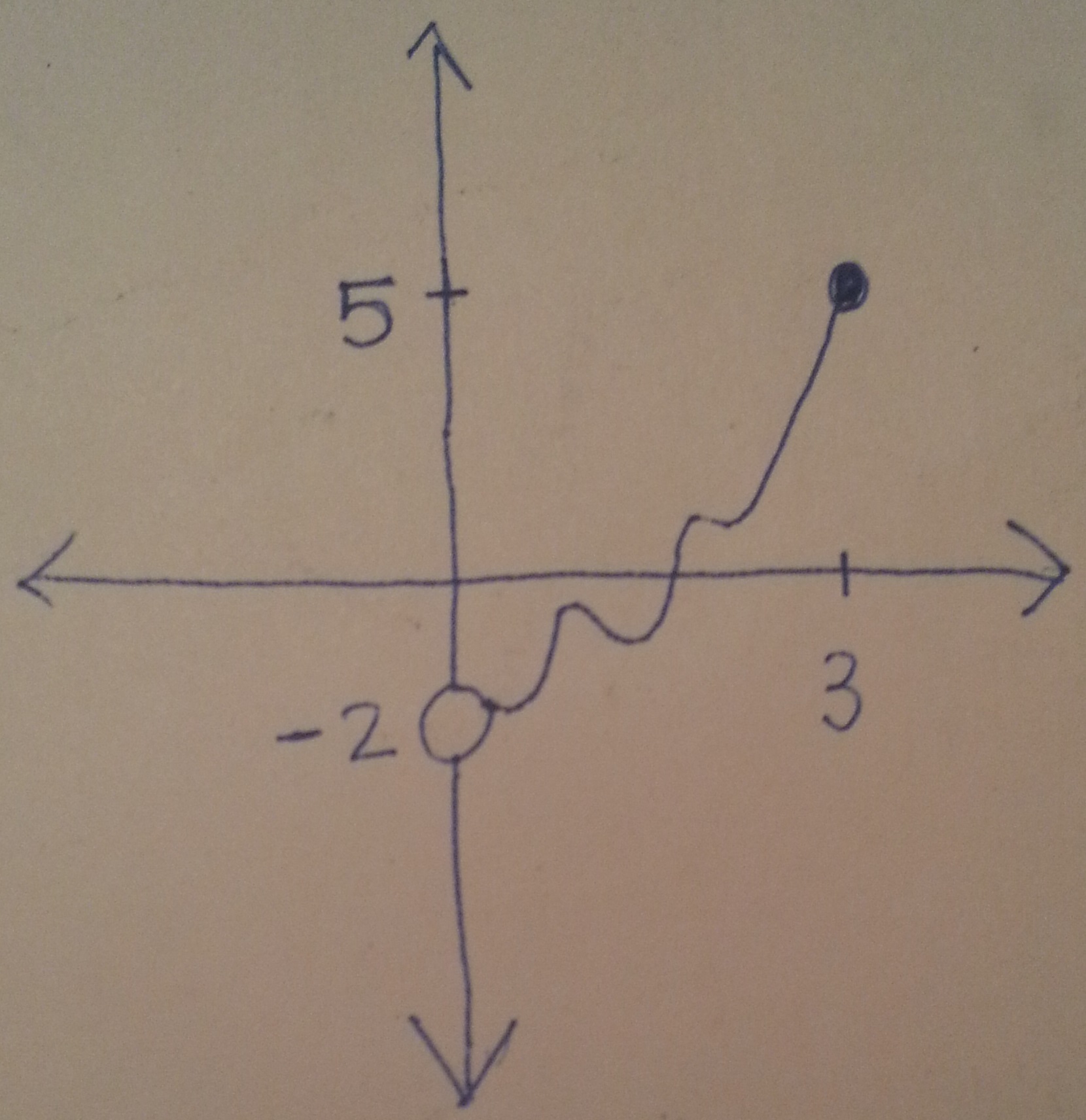
Solution: The domain is $(0,3]$ and the range is $(-2,5]$.
3. Find the slope of the line containing the points $(-2,7)$ and $(5,-3)$.
Solution: The slope is
$$\mathrm{slope}=m=\dfrac{-3-7}{5-(-2)} = -\dfrac{10}{7}.$$
4. What is the slope and the graph of the line $y=2x+3$?
Solution: The slope is $2$. The graph can be seen in the following image:
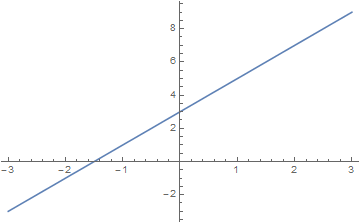
There are many ways to graph this yourself. For instance from the formula you know that the $y$-intercept is at $(0,3)$ and from the formula you may deduce that the $x$-intercept is at $\left( -\dfrac{3}{2}, 0 \right)$. Then you simply connect the dots.
5. Find the slope and $y$-intercept of the line described by $2x-3y=7$.
Solution The easiest way to do this is to rewrite the equation in the form $y=mx+b$. So solve for $y$ to get $y=\dfrac{2}{3}x-\dfrac{7}{3}$. Now it is clear that the slope is $\dfrac{2}{3}$ and the $y$-intercept is given by the point $\left( 0, -\dfrac{7}{3} \right)$.




