Back to the class
Section 5.1 #54: Determine if the function is one-to-one. If it is, find a formula for the inverse function:
$$f(x) = (x+5)^3.$$
Solution: First, the graph of this function is obtained by starting with the graph of $y=x^3$ and then shifting it to the left by $5$ units:
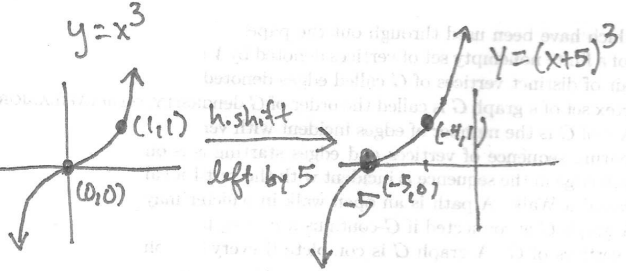 ,
,
which passes the "horizontal line test" and hence is one-to-one. So finding the inverse is possible. We have
$$y=(x+5)^3.$$
Solve for $x$ by first taking the cube root to get
$$\sqrt[3]{y}=\sqrt[3]{(x+5)^3}.$$
So,
$$\sqrt[3]{y}=x+5.$$
Therefore
$$\sqrt[3]{y}-5=x.$$
This means that $f^{-1}(y)=\sqrt[3]{y}-5$.
(note: writing $f^{-1}(x)=\sqrt[3]{x}-5$ is also ok -- you would arrive here if you do the "switch $x$ and $y$" thing)
Section 5.2 #34: Sketch the graph of
$$y=2^{x-1}-3.$$
Solution: This is the graph of $y=2^x$ shifted to the right by $1$ and then shifted down by $3$. Therefore we get:
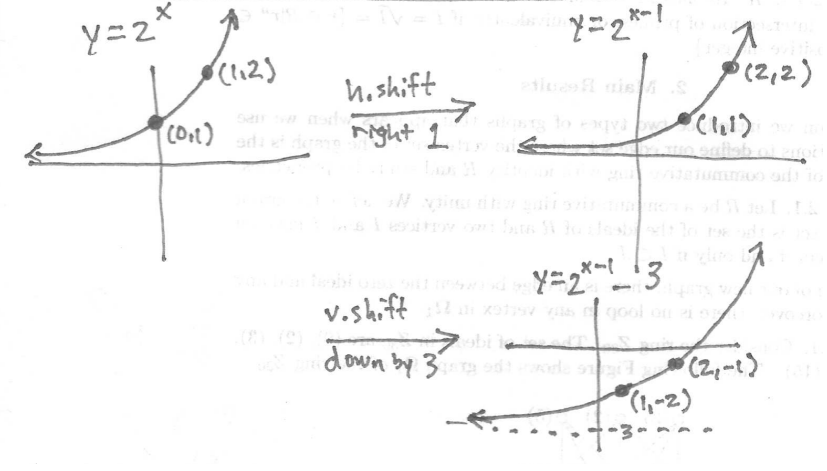
Section 5.3 #10: Find $\log_3(9)$.
Solution: The key is to recall that $\log_3(3^x)=x$, and so we want to rewrite $9$ as a power of $3$. This yields
$$\log_3(9)=\log_3(3^2)=2.$$
Section 5.3 #33: Find $\rm{ln} \left( \sqrt{e} \right)$.
Solution: Recall that $\ln$ is simply $\log_e$, where $e$ is the special number $e=2.71\ldots$. Therefore we want to express $\sqrt{e}$ as a power of $e$ and then take the logarithm:
$$\ln(\sqrt{e}) = \ln\left( e^{\frac{1}{2}} \right)=\dfrac{1}{2}.$$
Section 5.3 #46: Convert to an exponential equation:
$$t = \log_4(7).$$
Solution: We would like the logarithm on the right to disappear. Recall that $4^{\log_4(x)}=x$, and so we plug both sides of the equation into $4^x$ to get
$$4^t = 4^{\log_4(7)}$$
yielding
$$4^t = 7.$$
Section 5.3 #90: Sketch the graph of
$$y = \rm{ln}(x+1).$$
Solution: This is the graph of $y=\ln(x)$ shifted to the left by $1$ unit. Therefore,
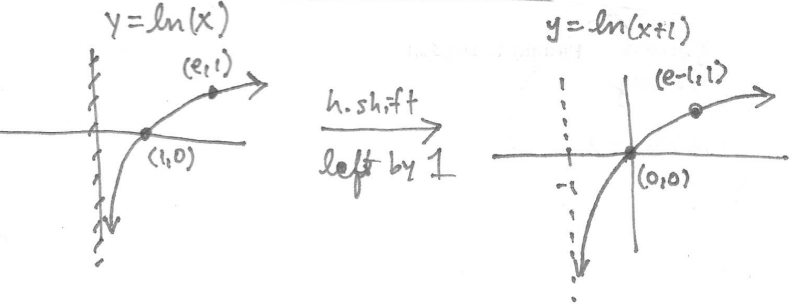



 ,
,
