Back to the class
Section 2.3 #23: Find $(f \circ g)(x)$ and $(g \circ f)(x)$ and the domain of each:
$$f(x)=\dfrac{4}{1-5x}; g(x)=\dfrac{1}{x}.$$
Solution: First compute
$$(f \circ g)(x) = f(g(x)) = f \left( \dfrac{1}{x} \right) = \dfrac{4}{1-\frac{5}{x}} = \dfrac{4x}{x-5}.$$
The domain of $(f \circ g)$ must lie in the domain of $g$, because we are first coputing $g(x)$ and then taking $f$ of $g(x)$. The domain of $g$ is all real numbers except $x=0$. Since the domain of $f$ is all real numbers except $\dfrac{1}{5}$ (set the denominator of $f$ equal to zero to see this), we must also throw out any value of $g(x)$ such that $g(x)=\dfrac{1}{5}$. This equation is $\dfrac{1}{x} = \dfrac{1}{5}$, which means $x=5$. Therefore the domain of $(f \circ g)$ is all real numbers except $0$ and $5$.
Now compute
$$(g \circ f)(x)=g(f(x)) = g\left( \dfrac{4}{1-5x} \right) = \dfrac{1}{\frac{4}{1-5x}} = \dfrac{1-5x}{4}.$$
The domain of $f$ is all real numbers except for $x=\dfrac{1}{5}$ and the domain of $g$ is all real numbers except $x=0$. Consequently, we must consider for which values of $x$ is $f(x)=5$, i.e. $\dfrac{4}{1-5x}=5.$ Multiply by $1-5x$ to get $4=5-25x$ implying $-25x = -1$, or $x = \dfrac{1}{25}$. Therefore the domain of $(g \circ f)$ is all real numbers except for $\dfrac{1}{5}$ and $\dfrac{1}{25}$.
Section 2.3 #40: Find $f(x)$ and $g(x)$ such that $h(x)=(f \circ g)(x)$, where
$$h(x)=\sqrt[3]{x^2-8}.$$
In other words, "decompose" the function $h$.
Solution: One way to proceed is to notice that the "outer" function is the cube root function and the "inner" function is $x^2-8$. So we can take $f(x)=\sqrt[3]{x}$ and $g(x)=x^2-8$ so that
$$(f \circ g)(x) = f(g(x)) = f(x^2-8) = \sqrt[3]{x^2-8}.$$
Section 2.4 #2: Determine visually whether the graph is symmetric with respect to the $x$-axis, the $y$-axis, or the origin:
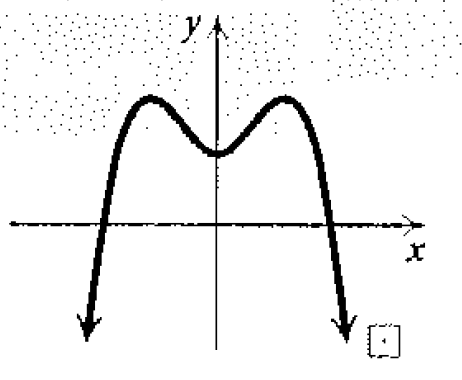
Solution: It is symmateric with respect to the $y$-axis.
Section 2.4 #27: Find the point that is symmetric to the point $(-5,6)$ with respect to the $x$-axis, the $y$-axis, and the origin.
Solution: The point symmetric to $(-5,6)$ about the $x$-axis is the point $(-5,-6)$. The point symmetric to $(-5,6)$ about the $y$-axis is $(5,6)$. The point symmetric to the origin is $(5,-6)$.
Section 2.4 #40: Determine whether the function $f(x)=7x^3+4x-1$ is even, odd, or neither.
Solution: Recall that a function is even means $f(-x)=f(x)$ for all $x$ and that a function is odd means $f(-x)=-f(x)$ for all $x$. Recall that
$$(-x)^3 = (-x)(-x)(-x) = -x^3.$$
First calculate
$$\begin{array}{ll}
f(-x) &= 7(-x)^3+4(-x)-1 \\
&= -7x^3 - 4x -1.
\end{array}$$
Now calculate
$$-f(x)=-(7x^3+4x-1) = -7x^3 - 4x + 1.$$
Since we see that $f(-x)$ is not the same as either $f(x)$ (the signs of the first two terms don't match) or $-f(x)$ (the sign of the third term does not match), we conclude that it is neither even nor odd.



