Back to the class
Section 2.1 #36: For the function
$$f(x) = \left\{ \begin{array}{ll}
3, & x \leq -2 \\
\frac{x}{2}+6, & x > -2,
\end{array} \right.$$
find the values $f(-5), f(-2), f(0),$ and $f(2)$.
Solution: Since $-5 \leq -2$, we compute
$$f(-5)=3.$$
Since $-2 \leq -2$, we compute
$$f(-2)=3.$$
Since $0 > -2$, we compute
$$f(0) = \dfrac{0}{2}+6 = 0+6 = 6.$$
Since $2 > -2$, we compute
$$f(2)=\dfrac{2}{2} + 6=1+6=7.$$
Section 2.1 #39: Graph the following function:
$$f(x) = \left\{ \begin{array}{ll}
\frac{x}{2}, & x < 0 \\
x+3, & x \geq 0.
\end{array} \right.$$
Solution: First consider the graph of $y=\dfrac{x}{2}$:
Now consider the graph of $y=x+3$:
Therefore the graph of the piecewise function is
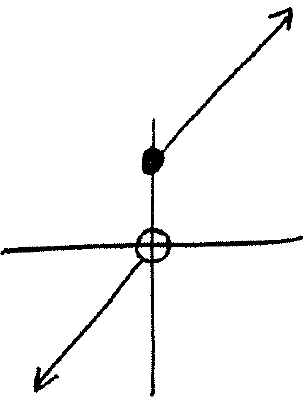
Section 2.2 #24: For the functions $f(x) = \sqrt{x}$ and $g(x)=\sqrt{2-x}$,
a.) Find the domain of $f$, $g$, $f+g$, $f-g$, $fg$, $ff$, $\dfrac{f}{g}$, and $\dfrac{g}{f}$.
b.) Find $(f+g)(x)$, $(f-g)(x)$, $(fg)(x)$, $(ff)(x)$, $\left( \dfrac{f}{g} \right)(x)$, and $\left( \dfrac{g}{f} \right)(x)$.
Solution:
a.) First note that the domain of $f$ is defined by the inequality $x \geq 0$, or as an interval,
$$\mathrm{dom}(f)=[0,\infty).$$
The domain of $g$ is defined by the inequality $2-x \geq 0$, which is equivalent to $2 \geq x$. We can write $2 \geq x$ as $x \leq 2$, or as an interval,
$$\mathrm{dom}(g)=(-\infty,2].$$
The domain of $f+g$, $f-g$, and $fg$ are all just the intersection of the domain of $f$ with the domain of $g$:
$$\mathrm{dom}(f+g) = \mathrm{dom}(f-g)=\mathrm{dom}(fg)=[0,\infty) \cap (-\infty,2] = [0,2].$$
The domain of $(ff)(x)$ will simply be the domain of $f$:
$$\mathrm{dom}(ff)=\mathrm{dom}(f)=[0,\infty).$$
The domain of $\left(\dfrac{f}{g} \right)(x)$ is the intersection of the domains of $f$ and $g$ and also taking away the $x$-values that cause $g(x)$ to be zero:
$$\mathrm{dom} \left( \dfrac{f}{g} \right) = [0,\infty) \cap (-\infty,2] \hspace{2pt} \mathrm{and \hspace{2pt} take \hspace{2pt} away \hspace{2pt}} 2=[0,2).$$
The domain of $\left( \dfrac{g}{f} \right)(x)$ is the intersection of the domains of $f$ and $g$ and also taking away the $x$-values that cause $f(x)$ to be zero:
$$\mathrm{dom} \left( \dfrac{g}{f} \right) = [0,\infty) \cap (-\infty,2] \hspace{2pt} \mathrm{and \hspace{2pt} take \hspace{2pt} away \hspace{2pt}} 0=(0,2].$$
b.) Compute
$$(f+g)(x) = f(x) + g(x) = \sqrt{x} + \sqrt{2-x},$$
$$(f-g)(x) = f(x)-g(x)=\sqrt{x}-\sqrt{2-x},$$
$$(fg)(x)=f(x)g(x)=\sqrt{x} \sqrt{2-x},$$
$$(ff)(x)=f(x)f(x)=\sqrt{x} \sqrt{x} = x,$$
$$\left( \dfrac{f}{g} \right)(x) = \dfrac{f(x)}{g(x)}=\dfrac{\sqrt{x}}{\sqrt{2-x}},$$
and
$$\left( \dfrac{g}{f} \right)(x) = \dfrac{g(x)}{f(x)} = \dfrac{\sqrt{2-x}}{\sqrt{x}}.$$
Section 2.2 #50: Compute the difference quotient $\dfrac{f(x+h)-f(x)}{h}$, where $f(x)=4x-1$.
Solution: Compute directly:
$$\begin{array}{ll}
\dfrac{f(x+h)-f(x)}{h} &= \dfrac{[4(x+h)-1] - [4x-1]}{h} \\
&= \dfrac{4x+4h-1-4x+1}{h} \\
&= \dfrac{4h}{h} \\
&= 4.
\end{array}$$





