Back to the class
Quiz 8
1.) What are the coordinates of $A$ and $B$ in the following graph?
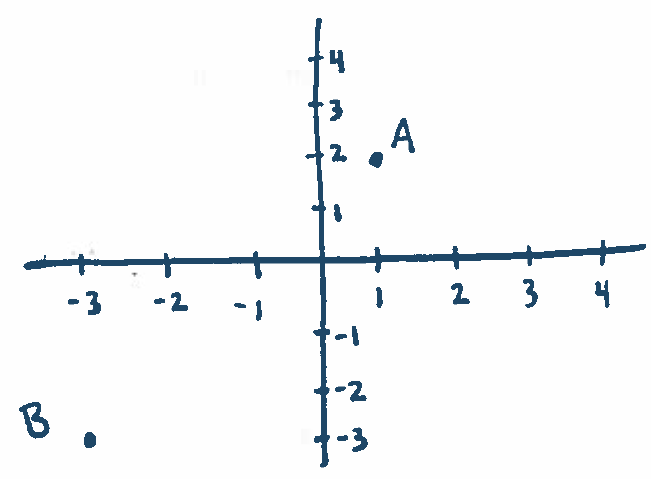
Solution: $A=(1,2)$ and $B=(-3,-3)$
2.) Plot the points $(3,5)$, $(6,-1)$, $(-2,7)$, and $(-3,-3)$.
Solution: 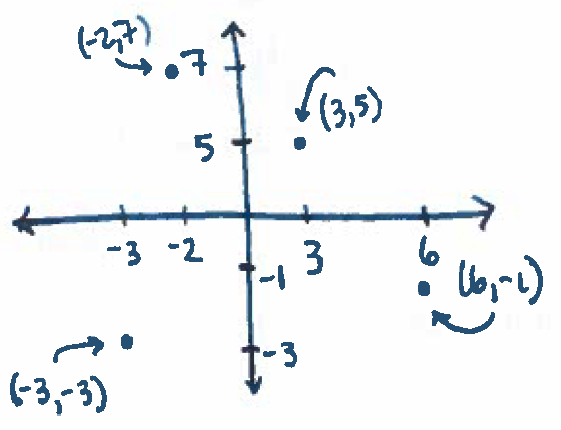
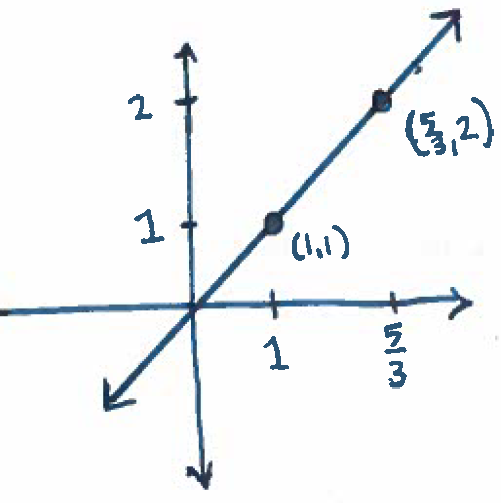
3.) Graph $3x-2y=1$.
Solution: Let us choose $x=1$ yielding the equation $3-2y=1$. Solve this equation for $y$ to get $y=1$. This means $(1,1)$ is a solution of this equation. Let us also choose $y=2$ yielding the equation $3x-4=1$. Solve this equation for $x$ to get $x=\dfrac{5}{3}$. This means that $\left( \dfrac{5}{3}, 2 \right)$ is a solution of the equation. We now plot the two solutions we have found on a coordinate plane and connect the dots to get the following graph:
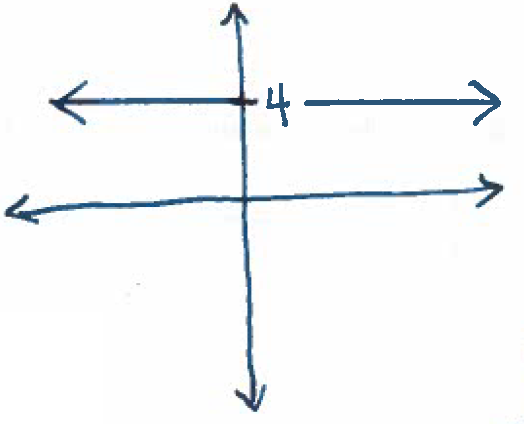
4.) Graph $y=4$.
Solution: We saw in class that lines of the form $y=a$ for some number $a$ describe a horizontal line at height $a$ (we *could* proceed similarly to above... but it is a "waste of time"). We get the following graph:
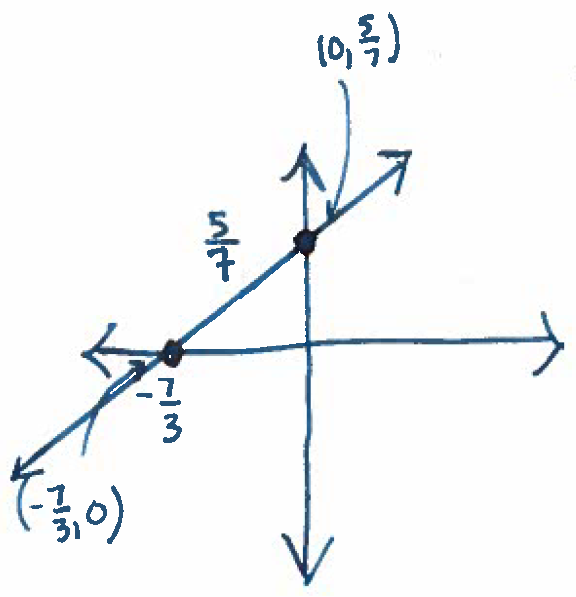
5.) Graph $5y=3x+7$.
Solution: Choose, say, $x=0$ to get the equation $5y=7$. Solve this for $y$ to get $y=\dfrac{7}{5}$. This means that $\left( 0, \dfrac{5}{7} \right)$ is a solution of the equation. Now choose, say, $y=0$ to get the equation $0=3x+7$. Solve this equation to get $x=-\dfrac{7}{3}$. This means that $\left( -\dfrac{7}{3}, 0 \right)$ is a solution of the equation. Now plot the two solutions and draw the line connecting them to get the following graph: