Back to the class
Quiz 22
1.) There is a concert for which VIP tickets cost $\$20$ and regular tickets cost $\$10$. A total of $75$ tickets were sold and $\$1050$ was earned. How many tickets of each type were sold?
Solution: Let $x$ represent the number of $\$20$ tickets and let $y$ represent the number of $\$10$ tickets. We are told $75$ total tickets are sold which gives us the equation
$$x+y=75.$$
The total income we earn by selling the $\$20$ tickets is $20x$ and the total income we earn by selling the $\$10$ tickets is $10y$. To say that we earned $\$1050$ gives us the equation
$$20x+10y=1050.$$
Therefore we have the system of equations
$$\left\{ \begin{array}{lll}
x+y &= 75 & \quad (i) \\
20x+10y&= 1050 & \quad (ii).
\end{array} \right.$$
Solve $(i)$ for $y$ to get $y=75-x$. Plug this into $(ii)$ to get
$$20x + 10(75-x) = 1050.$$
Distribute the $10$ to get
$$20x + 750 - 10x = 1050.$$
Combine like terms on the left and subtract $750$ to get
$$10x = 300.$$
Divide by $10$ to get
$$x = 30.$$
To find $y$, plug this value of $x$ into one of the equations -- plugging into equation $(i)$ is probably easier:
$$30+y=75.$$
Subtract $30$ to find
$$y = 45.$$
Therefore there were $30$ of the $\$20$ tickets sold and $45$ of the $\$10$ tickets sold.
2.) You want to mix Colombian coffee worth $\$10$ per pound and Turkish coffee worth $\$14$ per pound. How much of each should you mix together to get $30$ pounds of a coffee blend worth $\$12$ a pound?
Solution: Let $x$ represent the number of pounds of Colombian coffee and let $y$ represent the number of pounds of Turkish coffee. To say we want $30$ pounds of coffee in the end means we want
$$x+y=30.$$
The price of $x$ pounds of Colombian coffee is $10x$ and the price of $y$ pounds of Turkish coffee is $14y$. To say we want the mixture of $x+y$ pounds to be worth $\$12$ means that $12(x+y)$. This means the other equation is
$$10x+14y=12(x+y).$$
(NOTE: Since we already knew that $x+y=30$ you could also write that equationintead as $10x+14y=(12)(30)$ or $10x+14y=360$)
Therefore we have the system
$$\left\{ \begin{array}{lll}
x+y &= 30 & \quad (i) \\
10x+14y &= 12(x+y) & \quad (ii).
\end{array} \right.$$
We solve $(ii)$ for $x$: distribute the $12$ to get
$$10x+14y=12x+12y.$$
Subtract both sides by $10x$ and subtract both sides by $12y$ to get
$$2y = 2x.$$
Therefore
$$y=x.$$
Plug this into $(i)$ to get
$$x+x=30,$$
or
$$2x=30,$$
or
$$x=15.$$
Now find the value of $y$ and get $y=15$. Therefore if we mix $15$ pounds of Colombian coffee with $15$ pounds of Turkish coffee, we get $30$ pounds of a blend worth $\$12$ a pound.
3.) Graph
$$y \leq x+2.$$
Solution: First we will draw the line $y=x+2$ as a solid line:
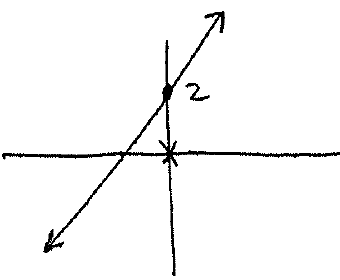
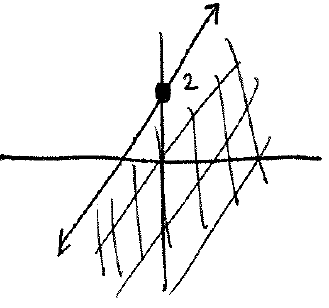
We will use the test point $(0,0)$ and plug it into the original inequality:
$$0 \leq 0 + 2$$
yielding
$$0 \leq 2,$$
which is true. Therefore we shade the half of the plane containing that tst point:
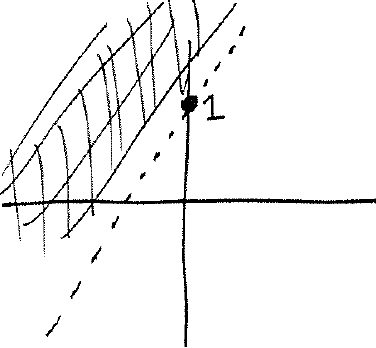
4.) Graph
$$y-1 > 2x.$$
Solution: First we will graph the line $y-1=2x$ with a dotted line (we don't have $\geq$ so we use dotted line). To easily see what line this is solve for $y$ to get $y=2x+1$. Draw this:
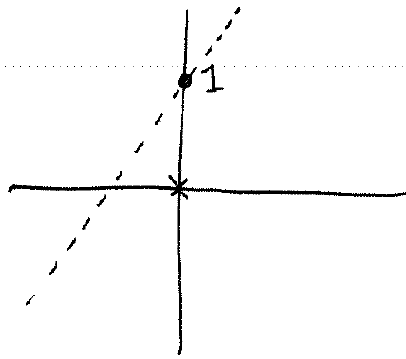
We will use the test point $(0,0)$ and plug it into the original inequality:
$$0-1 > 2(0).$$
Simplifying this yields
$$-1 > 0$$
which is false. Therefore we shade the half of the plane not containing the test point: