Back to the class
Problem A and pg.100 #3 are graded.
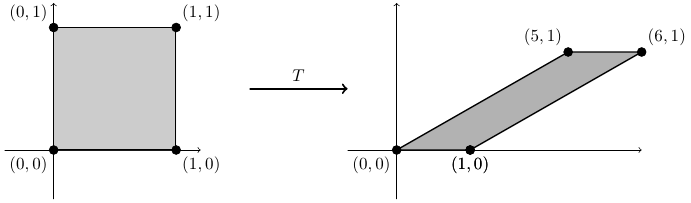
Problem A: Find the image of the square whose corners lie at the points $(0,0),(1,0),(0,1),(1,1)$ in the plane under the linear transformation
$$\begin{array}{ll}
T \colon \mathbb{R}^{2 \times 1} \rightarrow \mathbb{R}^{2 \times 1} \\
T(\vec{x})=A\vec{x},
\end{array}$$
where $A$ is the matrix $A=\begin{bmatrix} 1 & 5 \\ 0 & 1 \end{bmatrix}.$
Solution: We interpret the four corners of the square as vectors and plug them into the transformation $T$: first plug in $\begin{bmatrix} 0 \\ 0 \end{bmatrix}$ and get
$$\begin{array}{ll}
T \left( \begin{bmatrix} 0 \\ 0 \end{bmatrix} \right) = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{array}.$$
Now plug in $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ to get
$$T \left( \begin{bmatrix} 1 \\ 0 \end{bmatrix} \right) = \begin{bmatrix} 1 \\ 0 \end{bmatrix}.$$
Now plug in $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ to get
$$T \left( \begin{bmatrix} 0 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} 5 \\ 1 \end{bmatrix}$$
Finally, plug in $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ to get
$$T \left( \begin{bmatrix} 1 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} 6 \\ 1 \end{bmatrix}.$$
Thus you get the following picture:
#3,pg.100: Let $A = \left[ \begin{array}{ll}
2 & -5 \\
3 & -2
\end{array} \right]$. Compute $3I_2-A$ and $(3I_2)A$.
Solution: First we compute
$$\begin{array}{ll}
3I_2-A &= \left[ \begin{array}{ll}
3 & 0 \\
0 & 3
\end{array} \right] - \left[ \begin{array}{ll}
2 & -5 \\
3 & -2
\end{array} \right] \\
&= \left[ \begin{array}{ll}
1 & 5 \\
-3 & 5
\end{array} \right].
\end{array}$$
Now compute
$$\begin{array}{ll}
(3I_2)A &= \left[ \begin{array}{ll}
3 & 0 \\
0 & 3
\end{array} \right] \left[ \begin{array}{ll}
2 & -5 \\
3 & -2
\end{array} \right] \\
&= \left[ \begin{array}{ll}
6 & -15 \\
9 & -6
\end{array} \right]
\end{array}$$



