Back to undergraduate research page
Discrete special functions
The discrete hypergeometric series ${}_pF_q$ defined in this paper is $$ {}_pF_q(a_1,\ldots,a_p;b_1,\ldots,b_q;t,n,\xi) = \displaystyle\sum_{k=0}^{\infty} \dfrac{(a_1)_k\ldots(a_p)_k}{(b_1)_k\ldots(b_q)_k} \dfrac{t^{\underline{k}}}{k!},$$ where $(x)_k$ denotes a so-called "Pochhammer symbol.

---

---

Discrete Chebyshev polynomials
The classical Chebyshev polynomials (of the first kind) solve the differential equation \[ (1-t^2)y''-ty'+n^2y=0\] and have hypergeometric representation \[ \mathscr{T}_n(t) = {}_2F_1 \left( -n, n; \dfrac{1}{2}, \dfrac{1}{2}(1-t) \right).\]
Question 1: Define and solve the discrete analogue of this differential equation.
Question 2: Prove various formulas that the classical Chebyshev polynomials obey have discrete analogues.

---

---

Discrete sine-integral
The traditional sine-integral function $\mathscr{Si}$ is defined by $\mathscr{Si}(t)=\displaystyle\int_0^t \dfrac{\sin(t)}{t} \mathrm{d}t$. It obeys the differential equation $$ty^{\prime \prime \prime}+2y^{\prime \prime}+ty=0,$$ and it obeys the power series $$\mathscr{Si}(t) = \displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^{k-1}t^{2k-1}}{(2k-1)(2k-1)!}.$$ Question 1: Define and solve the discrete analogue of this differential equation.
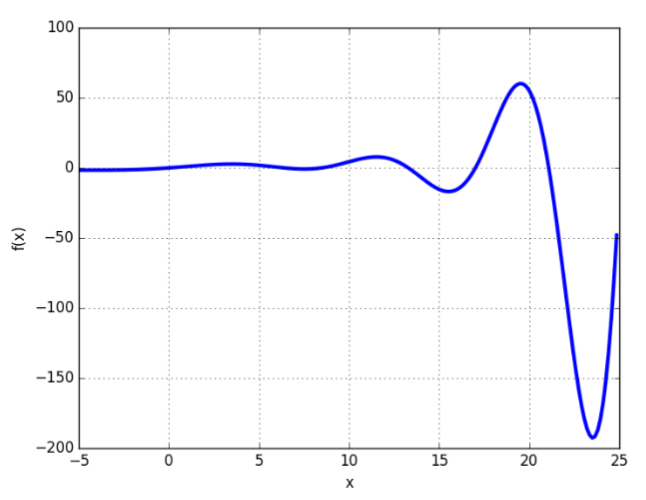
Answer 1: The discrete analogue is $$t\Delta^3 \mathrm{Si}(t-1) + 2 \Delta^2 \mathrm{Si}(t) + t\Delta \mathrm{Si}(t-1) = 0,$$ and the solution is $$\mathrm{Si}(t) = \displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^{k-1}t^{\underline{2k-1}}}{(2k-1)(2k-1)!}.$$ Question 2: Plot this function.
Answer 2: